题目内容
(本小题满分12分)在平面直角坐标系中,已知
 ,
,
 ,
, (
( ),
),
 ,O为坐标原点,若实数
,O为坐标原点,若实数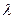 使向量
使向量 ,
, 和
和 满足:
满足: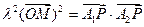 ,设点P的轨迹为
,设点P的轨迹为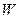 .
.
(Ⅰ)求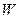 的方程,并判断
的方程,并判断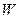 是怎样的曲线;
是怎样的曲线;
(Ⅱ)当 时,过点
时,过点 且斜率为1的直线与
且斜率为1的直线与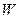 相交的另一个交点为
相交的另一个交点为 ,能否在直线
,能否在直线 上找到一点
上找到一点 ,恰使
,恰使 为正三角形?请说明理由.
为正三角形?请说明理由.

 ,
,
 ,
, (
( ),
),
 ,O为坐标原点,若实数
,O为坐标原点,若实数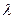 使向量
使向量 ,
, 和
和 满足:
满足: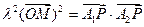 ,设点P的轨迹为
,设点P的轨迹为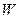 .
.(Ⅰ)求
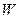 的方程,并判断
的方程,并判断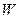 是怎样的曲线;
是怎样的曲线;(Ⅱ)当
 时,过点
时,过点 且斜率为1的直线与
且斜率为1的直线与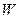 相交的另一个交点为
相交的另一个交点为 ,能否在直线
,能否在直线 上找到一点
上找到一点 ,恰使
,恰使 为正三角形?请说明理由.
为正三角形?请说明理由.(Ⅰ)W的方程为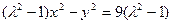 ,
,
①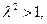 焦点在
焦点在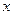 轴上的双曲线,
轴上的双曲线,
②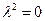 ,圆心在原点,半径为3的圆,
,圆心在原点,半径为3的圆,
③ 焦点在
焦点在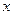 轴上的椭圆,
轴上的椭圆,
④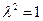 ,直线
,直线  ;
;
(Ⅱ)
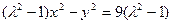 ,
,①
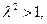 焦点在
焦点在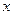 轴上的双曲线,
轴上的双曲线,②
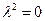 ,圆心在原点,半径为3的圆,
,圆心在原点,半径为3的圆,③
 焦点在
焦点在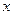 轴上的椭圆,
轴上的椭圆,④
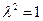 ,直线
,直线  ;
;(Ⅱ)
(Ⅰ)由已知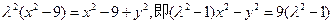 …… 2分
…… 2分
①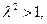 焦点在
焦点在 轴上的双曲线
轴上的双曲线
②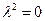 ,圆心在原点,半径为3的圆
,圆心在原点,半径为3的圆
③ 焦点在
焦点在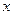 轴上的椭圆
轴上的椭圆
④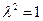 ,直线
,直线  ……………………… 6分
……………………… 6分
(Ⅱ) ,设直线
,设直线 方程为
方程为
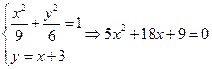 ……………………………10分
……………………………10分

 ,
,
在直线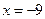 上,离
上,离 最短距离为6,
最短距离为6,
 无法形成正三角形 ……………………………12分
无法形成正三角形 ……………………………12分
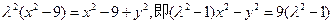 …… 2分
…… 2分①
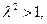 焦点在
焦点在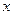 轴上的双曲线
轴上的双曲线②
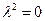 ,圆心在原点,半径为3的圆
,圆心在原点,半径为3的圆③
 焦点在
焦点在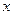 轴上的椭圆
轴上的椭圆④
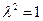 ,直线
,直线  ……………………… 6分
……………………… 6分(Ⅱ)
 ,设直线
,设直线 方程为
方程为
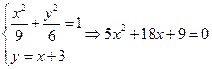 ……………………………10分
……………………………10分
 ,
, 在直线
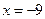 上,离
上,离 最短距离为6,
最短距离为6, 无法形成正三角形 ……………………………12分
无法形成正三角形 ……………………………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量 ,向量
,向量 ,
,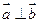 ,动点
,动点 的轨迹为E.
的轨迹为E. 为当
为当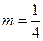 时轨迹E上的任意一点,定点
时轨迹E上的任意一点,定点 的坐标为(3,0),
的坐标为(3,0), 满足
满足 ,试求点
,试求点 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过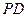 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。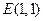 ,在动点
,在动点 、
、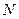 ,使
,使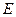 为
为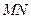 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。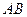 两端点
两端点 分别在
分别在 轴,
轴, 轴上滑动,
轴上滑动, 在线段
在线段
 的方程.
的方程. 且不垂直于坐标轴的直线
且不垂直于坐标轴的直线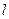 交轨迹
交轨迹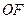 上是否存在一点
上是否存在一点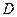 ,使得以
,使得以 为邻边的平行四边形为菱形?作出判断并证明.
为邻边的平行四边形为菱形?作出判断并证明.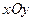 中,点M到点
中,点M到点 的距离之和是4,点M的轨迹是C,直线
的距离之和是4,点M的轨迹是C,直线 与轨迹C交于不同的两点P和Q.
与轨迹C交于不同的两点P和Q.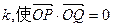 ?若存在,求出k的值;若不存在,请说明理由.
?若存在,求出k的值;若不存在,请说明理由. 是三角形的一个内角,且
是三角形的一个内角,且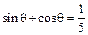 ,则方程
,则方程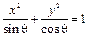 所表示的曲线是( )
所表示的曲线是( ) 轴上的椭圆
轴上的椭圆 轴上的椭圆
轴上的椭圆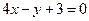 平行的抛物线
平行的抛物线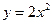 的切线方程是
的切线方程是
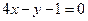

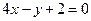
 在正方体
在正方体 的面
的面 及其边界运动,且到棱
及其边界运动,且到棱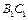 与棱
与棱 的距离相等,则动点
的距离相等,则动点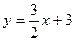 与曲线
与曲线 交点的个数是
交点的个数是