题目内容
以一个正方体顶点为顶点的四面体共有( ).
A.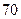 个 个 | B.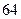 个 个 |
C.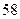 个 个 | D.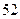 个 个 |
C
先不考虑四点共面,正方体 个顶点,从中每次取四点,构成
个顶点,从中每次取四点,构成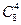 个四面体,
个四面体,
但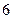 个表面和
个表面和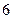 个对角面的四个顶点共面都不能构成四面体,所以四面体实际共有
个对角面的四个顶点共面都不能构成四面体,所以四面体实际共有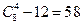 .
.
 个顶点,从中每次取四点,构成
个顶点,从中每次取四点,构成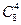 个四面体,
个四面体,但
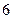 个表面和
个表面和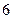 个对角面的四个顶点共面都不能构成四面体,所以四面体实际共有
个对角面的四个顶点共面都不能构成四面体,所以四面体实际共有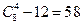 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
A.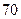 个 个 | B.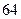 个 个 |
C.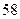 个 个 | D.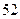 个 个 |
 个顶点,从中每次取四点,构成
个顶点,从中每次取四点,构成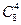 个四面体,
个四面体,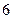 个表面和
个表面和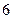 个对角面的四个顶点共面都不能构成四面体,所以四面体实际共有
个对角面的四个顶点共面都不能构成四面体,所以四面体实际共有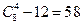 .
.
 阅读快车系列答案
阅读快车系列答案