题目内容
设球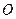 的半径是1,
的半径是1,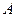 、
、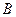 、
、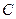 是球面上三点,已知
是球面上三点,已知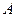 到
到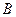 、
、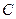 两点的球面距离都是
两点的球面距离都是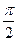 ,且二面角
,且二面角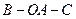 的大小是
的大小是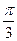 ,则从
,则从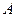 点沿球面经
点沿球面经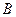 、
、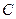 两点再回到
两点再回到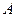 点的最短距离是( )
点的最短距离是( )
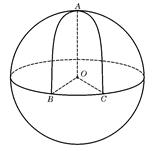
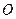 的半径是1,
的半径是1,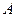 、
、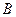 、
、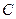 是球面上三点,已知
是球面上三点,已知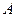 到
到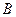 、
、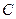 两点的球面距离都是
两点的球面距离都是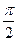 ,且二面角
,且二面角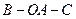 的大小是
的大小是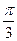 ,则从
,则从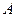 点沿球面经
点沿球面经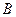 、
、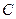 两点再回到
两点再回到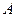 点的最短距离是( )
点的最短距离是( )
A.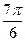 | B.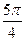 |
C.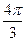 | D.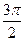 |
选C.
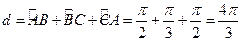 .本题考查球面距离.
.本题考查球面距离.
练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
题目内容
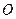 的半径是1,
的半径是1,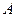 、
、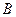 、
、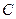 是球面上三点,已知
是球面上三点,已知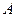 到
到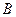 、
、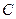 两点的球面距离都是
两点的球面距离都是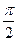 ,且二面角
,且二面角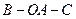 的大小是
的大小是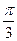 ,则从
,则从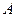 点沿球面经
点沿球面经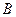 、
、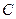 两点再回到
两点再回到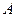 点的最短距离是( )
点的最短距离是( )
A.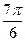 | B.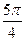 |
C.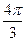 | D.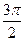 |
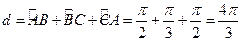 .本题考查球面距离.
.本题考查球面距离.
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案