题目内容
(本小题共12分)
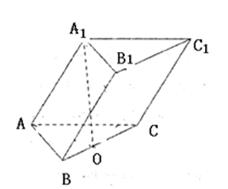
在三棱柱ABC—A1B1C1中,底面是边长为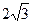 的正三角形,点A1在底面ABC上的射影O恰是BC的中点.
的正三角形,点A1在底面ABC上的射影O恰是BC的中点.
(1)求证:面A1AO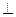 面BCC1B1;
面BCC1B1;
(2)当AA1与底面成45°角时,求二面角A1—AC—B的大小;
(3)若D为侧棱AA1上一点,当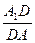 为何值时,BD⊥A1C1.
为何值时,BD⊥A1C1.

在三棱柱ABC—A1B1C1中,底面是边长为
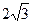 的正三角形,点A1在底面ABC上的射影O恰是BC的中点.
的正三角形,点A1在底面ABC上的射影O恰是BC的中点.(1)求证:面A1AO
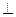 面BCC1B1;
面BCC1B1;(2)当AA1与底面成45°角时,求二面角A1—AC—B的大小;
(3)若D为侧棱AA1上一点,当
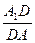 为何值时,BD⊥A1C1.
为何值时,BD⊥A1C1.arctan2,

证明:(1)连AO, ∵⊿ABC为正三角形, ∴AO⊥BC.

又∵A1O⊥面ABC,∴A1O⊥BC,∴BC⊥面A1AO
∴面A1AO⊥面BCC1B1 ………4分
(2)过O作OE⊥AC于E,连A1E,
∵A1O⊥面ABC,
∴ ,∴∠A1EO即为所求的平面角.
,∴∠A1EO即为所求的平面角.
∵正⊿ABC的边长为 ,∠A1AO=45°,
,∠A1AO=45°,
∴ .
.

∴二面角A1—AC—B的大小为arctan2 . …………8分
(3)过D作DF//A1O交AO于F,则DF⊥面ABC,
连BF,要使BD⊥A1C1,只要使BF⊥AC,
∵⊿ABC为正三角形,
∴只要F为△ABC的中心即可,
∴ 时,BD⊥A1C1. …………12分
时,BD⊥A1C1. …………12分

又∵A1O⊥面ABC,∴A1O⊥BC,∴BC⊥面A1AO
∴面A1AO⊥面BCC1B1 ………4分
(2)过O作OE⊥AC于E,连A1E,
∵A1O⊥面ABC,
∴
 ,∴∠A1EO即为所求的平面角.
,∴∠A1EO即为所求的平面角.∵正⊿ABC的边长为
 ,∠A1AO=45°,
,∠A1AO=45°,∴
 .
.
∴二面角A1—AC—B的大小为arctan2 . …………8分
(3)过D作DF//A1O交AO于F,则DF⊥面ABC,
连BF,要使BD⊥A1C1,只要使BF⊥AC,
∵⊿ABC为正三角形,
∴只要F为△ABC的中心即可,
∴
 时,BD⊥A1C1. …………12分
时,BD⊥A1C1. …………12分
练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 面ABC,BC
面ABC,BC
 平面
平面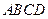 ,四边形
,四边形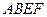 与
与
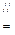
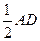 ,
,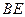
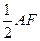 。
。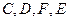 四点共面;
四点共面;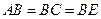 ,求二面角
,求二面角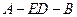 的大小。
的大小。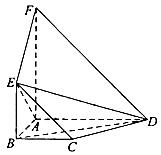
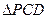 沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。
沿折线CD折成60°的二面角P—CD—A,设E,F,G分别是PD,PC,BC的中点。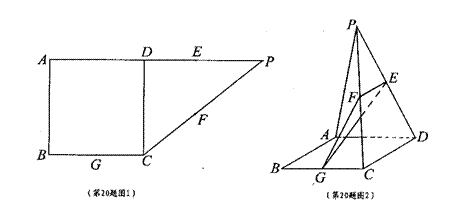
 个
个 个
个 个
个 个
个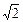 ,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
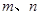 是两条不同的直线,
是两条不同的直线,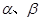 是两个不同的平面,有下列命题:
是两个不同的平面,有下列命题: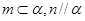 ,则
,则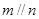 ; ②若
; ②若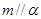 ,
,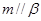 ,则
,则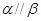 ;
;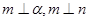 ,则
,则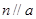 ; ④若
; ④若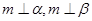 ,则
,则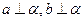 ,则
,则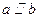 ;②若
;②若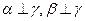 ,则
,则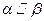 ;
;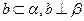 ,则
,则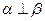 ;④若
;④若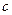 是
是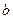 在
在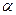 内的射影,
内的射影,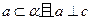 ,则
,则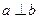 .
.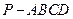 中,底面
中,底面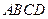 是矩形,
是矩形,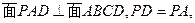
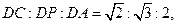
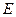 是
是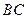 的中点,
的中点,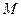 是
是 的中点。
的中点。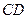 与
与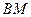 所成的角;(Ⅱ)求二面角
所成的角;(Ⅱ)求二面角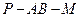 的大小。
的大小。