题目内容
12．如图为同样规格的黑、白两色正方体瓷砖铺设的图案，则按此规律第5个图案中需用黑色瓷砖的块数为（ ）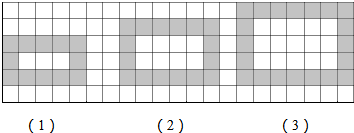
| A． | 22 | B． | 24 | C． | 26 | D． | 28 |
分析 本题通过观察前几个图案的规律进行归纳，在归纳时要抓住每个情况中反映的数量关系与序号之间的关系再进行概括．
解答 解：根据题目给出的图，我们可以看出：
1图中有黑色瓷砖12块，我们把12可以改写为3×4；
2图中有黑色瓷砖16块，我们把16可以改写为4×4；
3图中有黑色瓷砖20块，我们把20可以改写为5×4；
从具体中，我们要抽象出瓷砖的块数与图形的个数之间的关系，就需要对3、4、5这几个数字进行进一步的变形，用序列号1、2、3来表示，这样12，我们又可以写为12=（1+2）×4，16又可以写为16=（2+2）×4，20我们又可以写为20=（3+2）×4，注意到1、2、3恰好是图形的序列号，而2、4在图中都是确定的，
因此，我们可以从图中概括出第n个图有（n+2）×4，也就是，有4n+8块黑色的瓷砖．
当n=5时，4n+8=28，
故选：D
点评 归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
2．已知函数f（x）=（$\overrightarrow{a}$x+$\overrightarrow{b}$）2为偶函数，则向量$\overrightarrow{a}$，$\overrightarrow{b}$可以是（ ）
| A． | $\overrightarrow{a}$=（1，0），$\overrightarrow{b}$=（-1，1） | B． | $\overrightarrow{a}$=（-1，1），$\overrightarrow{b}$=（2，-2） | C． | $\overrightarrow{a}$=（1，1），$\overrightarrow{b}$=（2，-2） | D． | $\overrightarrow{a}$=（1，-1），$\overrightarrow{b}$=（0，-1） |
20．在△ABC中，BC=2，BC边上的高为$\sqrt{3}$，则∠BAC的范围为（ ）
| A． | （0，$\frac{π}{6}$] | B． | [$\frac{π}{6}$，$\frac{π}{4}$] | C． | （0，$\frac{π}{3}$] | D． | [$\frac{π}{3}$，$\frac{π}{2}$] |
根据某电子商务平台的调查统计显示，参与调查的1000位上网购物者的年龄情况如图显示．
17．已知数列{an}是等差数列，且a6+a7=10，则在（x-a1）（x-a2）…（x-a12）的展开式中，x11项的系数是（ ）
| A． | 60 | B． | -60 | C． | 30 | D． | -30 |
1．已知复数z=$\frac{2i}{1+i}$，则复数z的共轭复数$\overline{z}$是（ ）
| A． | -1+i | B． | -1-i | C． | 1-i | D． | 1+i |
2．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}x，x＞0}\\{{2}^{x}，x≤0}\end{array}\right.$，若f（a）=$\frac{1}{4}$，则a的值为（ ）
| A． | -2或$\frac{1}{4}$ | B． | $\root{4}{2}或-2$ | C． | -2 | D． | $\root{4}{2}$ |