题目内容
20.在△ABC中,BC=2,BC边上的高为$\sqrt{3}$,则∠BAC的范围为( )| A. | (0,$\frac{π}{6}$] | B. | [$\frac{π}{6}$,$\frac{π}{4}$] | C. | (0,$\frac{π}{3}$] | D. | [$\frac{π}{3}$,$\frac{π}{2}$] |
分析 设BC边的中垂线交直线L于A',作三角形A'BC的外接圆O,根据三角形外角定理,及圆周角定理的推论即可得到∠BAC的范围.
解答 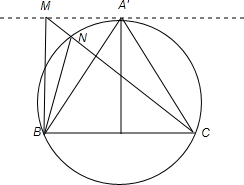 解:顶点A的轨迹是一条与BC边平行且到BC边距离为$\sqrt{3}$的直线L.
解:顶点A的轨迹是一条与BC边平行且到BC边距离为$\sqrt{3}$的直线L.
设BC边的中垂线交直线L于A',连接A'B,A'C.
三角形A'BC是等边三角形,且符合题设.则∠BA'C=$\frac{π}{3}$.
作三角形A'BC的外接圆O.
在直线L上任取一点M,连接MB、MC.设MB与圆O交于N点,连接CN.
因为同弧上的圆周角相等,三角形外角大于不相邻的内角知:
∠BMC<∠BNC=∠BA'C=$\frac{π}{3}$所以∠BAC的取值范围是(0,$\frac{π}{3}$].
故选:C.
点评 本题考查的知识点是圆周角定理的推论及三角形外角的性质,其中作BC边的中垂线交直线L于A',作三角形A'BC的外接圆O,为圆周角定理的使用创造条件是解答本题的关键,属于中档题.

练习册系列答案
相关题目
10.复数z满足|z-i|+|z+3|=10,则复数z对应点的集合表示的图形是( )
| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
12.如图为同样规格的黑、白两色正方体瓷砖铺设的图案,则按此规律第5个图案中需用黑色瓷砖的块数为( )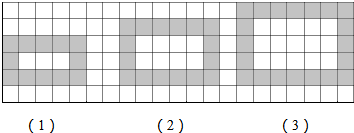

| A. | 22 | B. | 24 | C. | 26 | D. | 28 |
9.下列算法语句的处理功能是( )
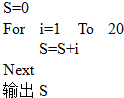
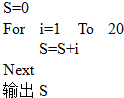
| A. | S=1+2+3+…+20 | B. | S=1+2+3+…+19 | C. | S=2+3+…+20 | D. | S=2+3+…+19 |
 如图,对于所给的算法中,若执行循环体的次数为1000,则原程序语言中实数a的取值范围是1000≤a<1001.
如图,对于所给的算法中,若执行循环体的次数为1000,则原程序语言中实数a的取值范围是1000≤a<1001.