题目内容
2.已知函数f(x)=($\overrightarrow{a}$x+$\overrightarrow{b}$)2为偶函数,则向量$\overrightarrow{a}$,$\overrightarrow{b}$可以是( )| A. | $\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(-1,1) | B. | $\overrightarrow{a}$=(-1,1),$\overrightarrow{b}$=(2,-2) | C. | $\overrightarrow{a}$=(1,1),$\overrightarrow{b}$=(2,-2) | D. | $\overrightarrow{a}$=(1,-1),$\overrightarrow{b}$=(0,-1) |
分析 由已知函数为偶函数得到向量$\overrightarrow{a}$,$\overrightarrow{b}$的数量积为0,由此选择.
解答 解:因为函数f(x)=($\overrightarrow{a}$x+$\overrightarrow{b}$)2=${\overrightarrow{a}}^{2}{x}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}x$为偶函数,所以$2\overrightarrow{a}•\overrightarrow{b}$=0;
观察各选项可得C满足;
故选C.
点评 本题考查了函数的奇偶性以及平面向量的数量积;关键是由已知函数为偶函数得到两个向量的数量积为0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知α∥β,λ∩β=b,λ∩α=a,那么a与b的关系是( )
| A. | 平行 | B. | 相交 | C. | 异面 |
10.复数z满足|z-i|+|z+3|=10,则复数z对应点的集合表示的图形是( )
| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
12.如图为同样规格的黑、白两色正方体瓷砖铺设的图案,则按此规律第5个图案中需用黑色瓷砖的块数为( )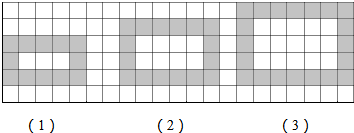

| A. | 22 | B. | 24 | C. | 26 | D. | 28 |
 如图,在平面直角坐标系内,已知A(1,0),B(-1,0)两点,且圆C的方程为x2+y2-6x-8y+21=0,点P为圆C上的动点.
如图,在平面直角坐标系内,已知A(1,0),B(-1,0)两点,且圆C的方程为x2+y2-6x-8y+21=0,点P为圆C上的动点. 如图所示的一个算法,其作用是输入x的值,输出相应y的值,若要使输出的y的值为正数,求输入的x值的取值范围.
如图所示的一个算法,其作用是输入x的值,输出相应y的值,若要使输出的y的值为正数,求输入的x值的取值范围.