题目内容

2．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}x，x＞0}\\{{2}^{x}，x≤0}\end{array}\right.$，若f（a）=$\frac{1}{4}$，则a的值为（　　）
A．-2或$\frac{1}{4}$B．$\root{4}{2}或-2$C．-2D．$\root{4}{2}$

分析 由f（a）=$\frac{1}{4}$得到关于a 的两个等式，在自变量范围内求值．

解答 解：因为f（a）=$\frac{1}{4}$，所以$lo{g}_{2}a=\frac{1}{4}$，或者${2}^{a}=\frac{1}{4}$，
解得a=$\root{4}{2}$或者a=-2；
故选B．

点评 本题考查了分段函数的函数值；只要由f（a）=$\frac{1}{4}$得到两个方程，分别解之即可；注意解得的自变量要在对应的自变量范围内．

练习册系列答案
相关题目
12．如图为同样规格的黑、白两色正方体瓷砖铺设的图案，则按此规律第5个图案中需用黑色瓷砖的块数为（　　）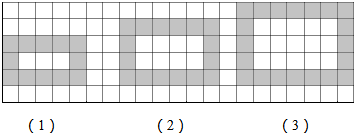
A．22B．24C．26D．28
13．已知函数f（x）=-3x2+a（5-a）x+b，a，b∈R．
（1）若不等式f（x）＞0的解集为（-1，3），求实数a，b的值；
（2）若b为常数，解关于a的不等式f（1）＜0．
10．已知x，y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤3}\\{2y≥x-3}\end{array}\right.$，则$\frac{y}{x}$的取值范围是[-1，2]．
17．设不等式组$\left\{\begin{array}{l}{0≤x≤6}\\{0≤x≤6}\end{array}\right.$表示的区域为A，不等式组$\left\{\begin{array}{l}{0≤x≤6}\\{x+y≥4}\end{array}\right.$表示的区域为B．
（1）在区域A中任取一点（x，y），求点（x，y）∈B的概率．
（2）若x，y分别表示甲、乙两人各掷一次骰子所得点数，求点（x，y）在区域B中的概率．
7．设函数f（x）=x2-klnx，k＞0．
（Ⅰ）若f（x）在点（1，f（1））处的切线过点（2，2），求k的值．
（Ⅱ）若f（x）的最小值小于零，证明f（x）在（1，$\sqrt{e}$]上仅有一个零点．
14．已知直线y=2x+1与圆x2+y2+mx=0没有公共点，则m的取值范围是（　　）
A．（4-2$\sqrt{5}$，4+2$\sqrt{5}$）B．（4-2$\sqrt{5}$，0）∪（0，4+2$\sqrt{5}$）C．（-4-2$\sqrt{5}$，-4+2$\sqrt{5}$）D．（-4-2$\sqrt{5}$，0）∪（0，-4+2$\sqrt{5}$）
11．某赛季，甲、乙两名篮球运动员都参加了10场比赛，比赛得分情况记录如下：
甲10304728461426114346
乙37213129193223252033
（Ⅰ）求甲10场比赛得分的中位数；
（Ⅱ）求乙10场比赛得分的方差．
12．在数列{an}中，已知a1=1，an+1-an=2，则{an}的通项公式是（　　）
A．an=2n+1B．an=2nC．an=2n-1D．an=2n+3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网