题目内容
4.古希腊毕达哥拉斯学派的数学家研究过各种多边形数,如三角形数1,3,6,10,…,第n个三角形数为$\frac{n(n+1)}{2}$=$\frac{1}{2}$n2+$\frac{1}{2}$n.记第n个k边形数为N(n,k)(k≥3),以下列出了部分k边形数中第n个数的表达式:三角形数 N(n,3)=$\frac{1}{2}$n2+$\frac{1}{2}$n 正方形数 N(n,4)=n2
五边形数 N(n,5)=$\frac{3}{2}{n^2}-\frac{1}{2}$n 六边形数 N(n,6)=2n2-n
可以推测N(n,k)的表达式,由此计算N(10,14)=550.
分析 观察已知式子的规律,并改写形式,归纳可得N(n,k)=$\frac{k-2}{2}$n2+$\frac{4-k}{2}$n,把n=10,k=14代入可得答案.
解答 解:原已知式子可化为:N(n,3)=$\frac{1}{2}$n2+$\frac{1}{2}$n=$\frac{3-2}{2}{n}^{2}+\frac{4-3}{2}n$;
N(n,4)=n2=$\frac{4-2}{2}{n}^{2}+\frac{4-4}{2}n$;
N(n,5)=$\frac{3}{2}{n^2}-\frac{1}{2}$n
N(n,6)=2n2-n=$\frac{5-2}{2}{n}^{2}+\frac{4-5}{2}n$
…
由归纳推理可得N(n,k)=$\frac{k-2}{2}$n2+$\frac{4-k}{2}$n,
故N(10,14)=$\frac{14-2}{2}{×10}^{2}+\frac{14-3}{2}×10$=550,
故答案为:550
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
12.如图为同样规格的黑、白两色正方体瓷砖铺设的图案,则按此规律第5个图案中需用黑色瓷砖的块数为( )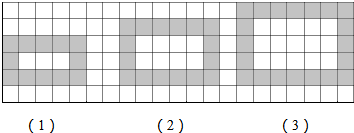

| A. | 22 | B. | 24 | C. | 26 | D. | 28 |
19.直线ax+by+c=0与圆x2+y2=9相交于两点M、N,若c2=a2+b2,则|MN|=( )
| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{10}$ | D. | $\sqrt{10}$ |
9.下列算法语句的处理功能是( )
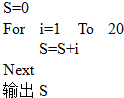
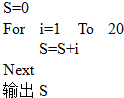
| A. | S=1+2+3+…+20 | B. | S=1+2+3+…+19 | C. | S=2+3+…+20 | D. | S=2+3+…+19 |
14.已知直线y=2x+1与圆x2+y2+mx=0没有公共点,则m的取值范围是( )
| A. | (4-2$\sqrt{5}$,4+2$\sqrt{5}$) | B. | (4-2$\sqrt{5}$,0)∪(0,4+2$\sqrt{5}$) | C. | (-4-2$\sqrt{5}$,-4+2$\sqrt{5}$) | D. | (-4-2$\sqrt{5}$,0)∪(0,-4+2$\sqrt{5}$) |
 如图所示的一个算法,其作用是输入x的值,输出相应y的值,若要使输出的y的值为正数,求输入的x值的取值范围.
如图所示的一个算法,其作用是输入x的值,输出相应y的值,若要使输出的y的值为正数,求输入的x值的取值范围. 如图,对于所给的算法中,若执行循环体的次数为1000,则原程序语言中实数a的取值范围是1000≤a<1001.
如图,对于所给的算法中,若执行循环体的次数为1000,则原程序语言中实数a的取值范围是1000≤a<1001.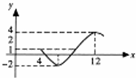 +c(A>0,ω>0,φ>0)图象的一部分.
+c(A>0,ω>0,φ>0)图象的一部分.