题目内容
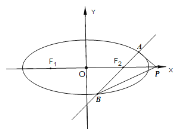
【题目】椭圆![]() 的焦点为
的焦点为![]() 和
和![]() ,过
,过![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点,过
两点,过![]() 作与
作与![]() 轴垂直的直线
轴垂直的直线![]() ,又知点
,又知点![]() ,直线
,直线![]() 记为
记为![]() ,
,![]() 与
与![]() 交于点
交于点![]() .设
.设![]() ,已知当
,已知当![]() 时,
时,![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求证:无论![]() 如何变化,点
如何变化,点![]() 的横坐标是定值,并求出这个定值.
的横坐标是定值,并求出这个定值.
【答案】(Ⅰ)![]() ;(Ⅱ)定值为3
;(Ⅱ)定值为3
【解析】
(Ⅰ)设椭圆的方程为![]()
![]() ,当
,当![]() 时,不妨设
时,不妨设![]() ,则
,则![]() ,由椭圆的定义得
,由椭圆的定义得![]() ,从而
,从而![]() ,可得点A在y轴上,不妨设
,可得点A在y轴上,不妨设![]() ,由
,由![]() 可得
可得![]() ,将B代入椭圆方程即可;
,将B代入椭圆方程即可;
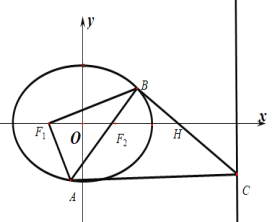
(Ⅱ)设直线AB的方程为![]() ,
,![]() ,联立椭圆方程可得
,联立椭圆方程可得![]() ,进一步可得
,进一步可得![]() ,
,![]() ,利用点斜式可得BH的方程以及直线
,利用点斜式可得BH的方程以及直线![]() 的方程,解方程组即可.
的方程,解方程组即可.
(Ⅰ)设椭圆的方程为![]() ,其中
,其中![]() ,由已知,当
,由已知,当![]() 时,不妨设
时,不妨设![]() ,
,
则![]() ,又
,又![]() ,所以
,所以![]() ,由椭圆的定义得
,由椭圆的定义得![]() ,
,
从而![]() ,此时点A在y轴上,不妨设
,此时点A在y轴上,不妨设![]() ,
,
从而由已知条件![]() 可得
可得![]() ,解得
,解得![]() ,
,
故![]() ,代入椭圆方程,解得
,代入椭圆方程,解得![]() ,所以
,所以![]() ,
,
故所求椭圆方程为![]() .
.
(Ⅱ)设直线AB的方程为![]() ,
,![]() ,将
,将![]() 代入椭圆
代入椭圆
![]() 中,得
中,得![]() ,即
,即![]() ,
,
![]() ,所以
,所以![]() ,
,
由已知,![]() ,直线BH的斜率
,直线BH的斜率 ,
,
所以直线BH的方程为![]() ,而直线
,而直线![]() 的方程为
的方程为![]() ,代入
,代入![]() ,
,
解得![]() ,故点
,故点![]() 的横坐标是定值3.
的横坐标是定值3.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
【题目】已知某校运动会男生组田径综合赛以选手三项运动的综合积分高低决定排名.具体积分规则如表1所示,某代表队四名男生的模拟成绩如表2.
表1 田径综合赛项目及积分规则
项目 | 积分规则 |
| 以 |
跳高 | 以 |
掷实心球 | 以 |
表2 某队模拟成绩明细
姓名 | 100米跑(秒) | 跳高(米) | 掷实心球(米) |
甲 |
|
|
|
乙 |
|
|
|
丙 |
|
|
|
丁 |
|
|
|
根据模拟成绩,该代表队应选派参赛的队员是:( )
A.甲B.乙C.丙D.丁