题目内容
已知数列 满足
满足 .
.
(1)求证:数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式
的通项公式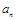 ;
;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,求证:对任意
,求证:对任意 ,有
,有 成立.
成立.
 满足
满足 .
.(1)求证:数列
 是等比数列,并求数列
是等比数列,并求数列 的通项公式
的通项公式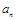 ;
;(2)设
 ,数列
,数列 的前
的前 项和为
项和为 ,求证:对任意
,求证:对任意 ,有
,有 成立.
成立.(1) ;(2)见解析。
;(2)见解析。
 ;(2)见解析。
;(2)见解析。试题分析:(1)根据
 对数列
对数列 的通项公式
的通项公式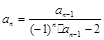 进行配凑,根据定义去证明;(2)结合(1)及三角函数的周期性得
进行配凑,根据定义去证明;(2)结合(1)及三角函数的周期性得 然后放缩构造等比数列进行求和,
然后放缩构造等比数列进行求和,(1)
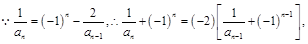
又
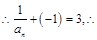 数列
数列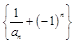 是首项为3,公比为-2的等比数列. 4′
是首项为3,公比为-2的等比数列. 4′从而
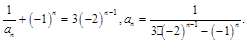 6′
6′(2)
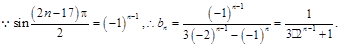 8′
8′当
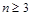 时,则
时,则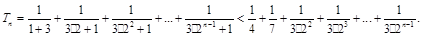
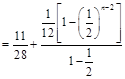
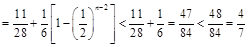 12′
12′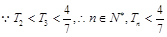 14′
14′
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
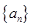 满足
满足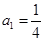 ,
,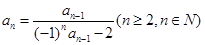 .
.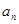 ;
;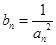 ,求数列
,求数列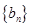 的前n项和
的前n项和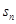 ;
;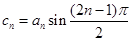 ,数列
,数列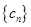 的前n项和为
的前n项和为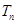 .求证:对任意的
.求证:对任意的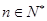 ,
,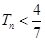 .
.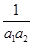 +
+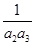 +…+
+…+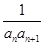 的结果可化为( )
的结果可化为( )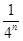
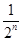
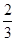 (1-
(1-



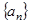 的前
的前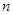 项和为
项和为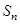 ,已知
,已知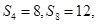 则
则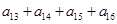 的值为 .
的值为 .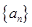 的前
的前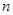 项和为
项和为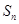 ,且
,且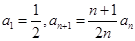 .
.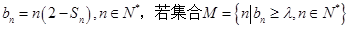 恰有5个元素,求实数
恰有5个元素,求实数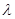 的取值范围.
的取值范围.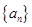 满足
满足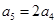 ,
,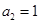 ,数列
,数列 项和
项和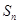 ,则
,则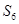 = .
= .