题目内容
19.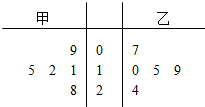 某区今年春季运动会共有5场篮球比赛,其中甲、乙两运动员得分的茎叶图如图所示.
某区今年春季运动会共有5场篮球比赛,其中甲、乙两运动员得分的茎叶图如图所示.(Ⅰ)求甲、乙两名队员得分的平均值和方差,并判断哪一个队员的成绩更稳定;
(Ⅱ)在甲队员的得分中任选两个得分,求恰有一个得分不低于平均分的概率.
分析 (Ⅰ)由茎叶图可知,甲、乙的得分,根据平均数个方差的计算公式计算并判断即可;
(Ⅱ)在甲队员的得分中任意抽取两个得分的情形为10种,而恰有1个分数不低于平均分(15分)的有6种,根据概率公式计算即可.
解答 解:(Ⅰ)由茎叶图可知,甲、乙的得分分别为:
甲:9,11,12,15,28; 乙:7,10,15,19,24.
∴$\overline{x_甲}=\frac{1}{5}(9+11+12+15+28)=15$,
$\overline{x_乙}=\frac{1}{5}(7+10+15+19+24)=15$.
∴甲、乙的平均值相同.
${s_甲}^2=\frac{1}{5}[(9-15{)^2}+(11-15{)^2}+(12-15{)^2}+(15-15{)^2}+(28-15{)^2}]=46$,
${s_乙}^2=\frac{1}{5}[(7-15{)^2}+(10-15{)^2}+(15-15{)^2}+(19-15{)^2}+(24-15{)^2}]=37.2$,
∵${s_甲}^2>{s_乙}^2$,故乙队员的成绩比甲队员的成绩稳定.
(Ⅱ)在甲队员的得分中任意抽取两个得分的情形为:(9,11),(9,12),(9,15),(9,28),(11,12),(11,15),(11,28),(12,15),(12,28),(15,28)
共有10种情形.
而恰有1个分数不低于平均分(15分)的有:(9,15),(9,28),(11,15),(11,28),(12,15),(12,28)
共有6种情形
∴所求概率$P=\frac{6}{10}=0.6$.
点评 本题考查了茎叶图,平均数,方差,古典概型的概率问题,属于基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
10.将1~9这9个数平均分成3组,则每组的3个数都成等差数列的分组方法的种数是( )
| A. | 3 | B. | 5 | C. | 7 | D. | 9 |
11.已知α∈(π,$\frac{3}{2}$π),cosα=-$\frac{4}{5}$,则tanα=( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{3}{4}$ |
9.若$\frac{1}{27}$≤x≤9,则f(x)=log3$\frac{x}{27}$•log3(3x)( )
| A. | 有最小值-$\frac{32}{9}$,最大值-3 | B. | 有最小-4,最大值12 | ||
| C. | 有最小值-$\frac{32}{9}$,无最大值 | D. | 无最小值,有最大值12 |