题目内容
4.一位模型赛车手遥控一辆赛车,沿直线向正东方向前行1m,逆时针方向旋转α°,继续沿直线向前行进1m,再逆时针旋转α°,按此方法继续操作下去.(1)按1:100的比例作图说明当α=60°时,操作几次赛车的位移为零;
(2)按此操作使赛车能回到出发点,α应满足什么条件?请写出两个.
分析 (1)转一圈为360°,二圈为720°,用360°除以60°即得到操作次数.
(2)用正多边形的知识得到n(180°-α)=(n-2)180°,易得操作次数n=$\frac{360°}{α}$,n为不小于3的整数.
解答 解:(1)360°÷60°=6
故应该操作6次赛车的位移为零.
(2)要使赛车能回到出发点,只需赛车的位移为零,
用正多边形的知识得到n(180°-α)=(n-2)180°,
解得:n=$\frac{360°}{α}$,n为不小于3的整数.
如α=45°,则n=8,即操作8次回到起点,
又如α=72°,则n=5,即操作5次回到起点.
点评 本题主要考查正多边形外角的特点,每个外角都相等.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
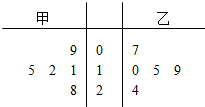 某区今年春季运动会共有5场篮球比赛,其中甲、乙两运动员得分的茎叶图如图所示.
某区今年春季运动会共有5场篮球比赛,其中甲、乙两运动员得分的茎叶图如图所示.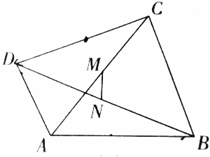 如图,四边形ABCD的对角线AC、BD的中点分别为M、N,求证:$\frac{1}{2}$|AB-CD|≤MN≤$\frac{1}{2}$(AB+CD).
如图,四边形ABCD的对角线AC、BD的中点分别为M、N,求证:$\frac{1}{2}$|AB-CD|≤MN≤$\frac{1}{2}$(AB+CD).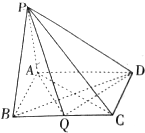 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=aBC(a>0).
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=aBC(a>0).