题目内容
11．已知α∈（π，$\frac{3}{2}$π），cosα=-$\frac{4}{5}$，则tanα=（ ）| A． | $\frac{4}{3}$ | B． | $\frac{3}{4}$ | C． | -$\frac{4}{3}$ | D． | -$\frac{3}{4}$ |
分析 由α的范围及cosα的值，利用同角三角函数间的基本关系求出sinα的值，即可求出tanα的值．
解答 解：∵α∈（π，$\frac{3}{2}$π），cosα=-$\frac{4}{5}$，
∴sinα=-$\sqrt{1-co{s}^{2}α}$=-$\frac{3}{5}$，
则tanα=$\frac{sinα}{cosα}$=$\frac{3}{4}$，
故选：B．
点评 此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
2．设p，q是两个命题，则“p，q均为假命题”是“p∧q为假命题”的（ ）条件．
| A． | 充分不必要 | B． | 必要不充分 | ||
| C． | 充分必要 | D． | 既不充分也不必要 |
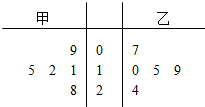某区今年春季运动会共有5场篮球比赛，其中甲、乙两运动员得分的茎叶图如图所示．