题目内容
12.已知f(x)=x|x-a|-$\frac{1}{4}$,x∈R.(1)a=1时,指出f(x)单调区间和奇偶性;
(2)a=1时,求y=f(2x)零点;
(3)对任何x∈[0,1],不等式f(x)<0恒成立,求a的取值范围.
分析 (1)当a=1时,利用分段函数的图象得出函数的单调区间和函数f(x)的奇偶性;
(2)当a=1时,f(x)=x|x-1|-$\frac{1}{4}$,欲求函数y=f(2x)的零点,即求对应方程的根.由f(2x)=0解得x的值即可;
(3)当x=0时,a取任意实数,不等式f(x)<0恒成立,故只需考虑x∈(0,1],此时原不等式变为$|x-a|<\frac{1}{4x}$,即$x-\frac{1}{4x}<a<x+\frac{1}{4x}$.再构造函数,研究其最值即可得出实数a的取值范围.
解答 解:(1)当a=1时,f(x)=x|x-a|-$\frac{1}{4}$=x|x-1|-$\frac{1}{4}$,
则当x≥1时,f(x)=x|x-1|-$\frac{1}{4}$=x2-x-$\frac{1}{4}$=(x-$\frac{1}{2}$)2-$\frac{1}{2}$,
当x<1时,f(x)=x|x-1|-$\frac{1}{4}$=-x2+x-$\frac{1}{4}$=-(x-$\frac{1}{2}$)2,
∴函数的单调递减区间为$[{\frac{1}{2},1}]$,函数的递增区间为(-∞,$\frac{1}{2}$]和[1,+∞),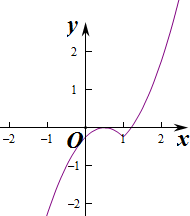
函数f(x)既不是奇函数也不是偶函数.
(2)当a=1时,$f(x)=x|x-1|-\frac{1}{4}$,
由f(2x)=0得${2^x}|{2^x}-1|-\frac{1}{4}=0$,
即$\left\{{\begin{array}{l}{{2^x}≥1}\\{{{({2^x})}^2}-{2^x}-\frac{1}{4}=0}\end{array}}\right.$或$\left\{{\begin{array}{l}{{2^x}<1}\\{{{({2^x})}^2}-{2^x}+\frac{1}{4}=0}\end{array}}\right.$,
解得${2^x}=\frac{{1+\sqrt{2}}}{2}或{2^x}=\frac{{1-\sqrt{2}}}{2}(舍),或{2^x}=\frac{1}{2}$
所以$x={log_2}\frac{{1+\sqrt{2}}}{2}={log_2}(1+\sqrt{2})-1$或x=-1.
(3)当x=0时,a取任意实数,不等式f(x)<0恒成立,
故只需考虑x∈(0,1],此时原不等式变为$|x-a|<\frac{1}{4x}$
即$x-\frac{1}{4x}<a<x+\frac{1}{4x}$,
故${(x-\frac{1}{4x})_{max}}<a<{(x+\frac{1}{4x})_{min}},x∈({0,1}]$
又函数$g(x)=x-\frac{1}{4x}$在(0,1]上单调递增,
∴${(x-\frac{1}{4x})_{max}}=g(1)=\frac{3}{4}$,
函数$h(x)=x+\frac{1}{4x}$在$({0,\frac{1}{2}}]$上单调递减,在$[{\frac{1}{2},1}]$上单调递增,
∴${(x+\frac{1}{4x})_{min}}=h(\frac{1}{2})=1$;
∴$\frac{3}{4}<a<1$,
即实数a的取值范围是$({\frac{3}{4},1})$.
点评 本题以分段函数为载体,考查函数的奇偶性单调性、恒成立等问题,利用数形结合是解决本题的关键.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案| A. | -3 | B. | 1 | C. | -3或1 | D. | 3 |