Question

20．若直线y=2a与函数y=|a^x-1|+1（a＞0且a≠1）的图象有两个公共点，则a的取值范围是$\frac{1}{2}$＜a＜1．

Answer 1

分析 先分：①0＜a＜1和a＞1时两种情况，作出函数y=|a^x-1|图象，再由直线y=2a与函数y=|a^x-1|+1（a＞0且a≠1）的图象有两个公共点，即直线y=2a-1与函数y=|a^x-1|（a＞0且a≠1）的图象有两个公共点，作出直线，移动直线，用数形结合求解．

解答 解：①当0＜a＜1时，作出函数y=|a^x-1|图象：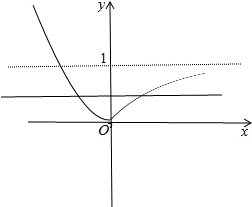

若直线y=2a与函数y=|a^x-1|+1（a＞0且a≠1）的图象有两个公共点，
则直线y=2a-1与函数y=|a^x-1|（a＞0且a≠1）的图象有两个公共点
由图象可知0＜2a-1＜1，
∴$\frac{1}{2}$＜a＜1．
②：当a＞1时，作出函数y=|a^x-1|图象：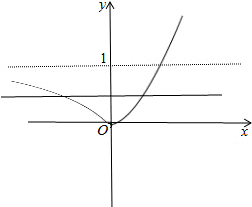

若直线y=2a与函数y=|a^x-1|+1（a＞0且a≠1）的图象有两个公共点，
则直线y=2a-1与函数y=|a^x-1|（a＞0且a≠1）的图象有两个公共点
由图象可知0＜2a-1＜1，
此时无解．
综上：a的取值范围是$\frac{1}{2}$＜a＜1．
故答案为：$\frac{1}{2}$＜a＜1

点评 本题主要考查指数函数的图象和性质，主要涉及了函数的图象变换及函数的单调性，同时，还考查了数形结合的思想方法．