题目内容
(12分)已知二次函数f (x)=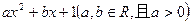 ,设方程f (x)
,设方程f (x)
=x的两个实根为x1和x2.
(1)如果x1<2<x2<4,且函数f (x)的对称轴为x=x0,求证:x0>—1;
(2)如果∣x1∣<2,,∣x2—x1∣=2,求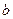 的取值范围.
的取值范围.
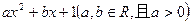 ,设方程f (x)
,设方程f (x)=x的两个实根为x1和x2.
(1)如果x1<2<x2<4,且函数f (x)的对称轴为x=x0,求证:x0>—1;
(2)如果∣x1∣<2,,∣x2—x1∣=2,求
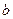 的取值范围.
的取值范围.解:(1)设g(x)=" f" (x)—x
=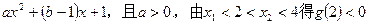 ,且g(4)>0,即
,且g(4)>0,即
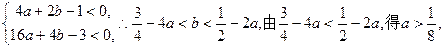
∴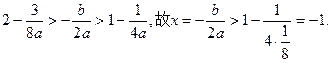
(2)由g(x)=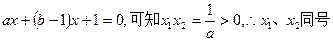 .
.
①若0<x1<2,则x2一x1=2,即x2=x1+2>2,∴g(2)=4a+2b—1<0,
又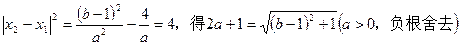 ,代入上式得
,代入上式得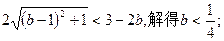
②若一2<x1<0,则x2=一2+x1<一2,∴g(一2)<0,即4a-2b+3<0,同理可求得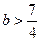 .
.
故当0<x1<2时,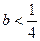 ;当一2<x1<0时,
;当一2<x1<0时,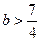 .
.
=
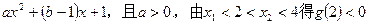 ,且g(4)>0,即
,且g(4)>0,即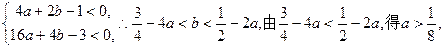
∴
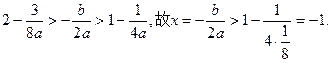
(2)由g(x)=
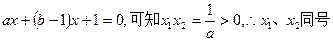 .
.①若0<x1<2,则x2一x1=2,即x2=x1+2>2,∴g(2)=4a+2b—1<0,
又
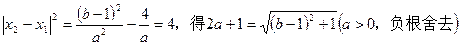 ,代入上式得
,代入上式得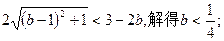
②若一2<x1<0,则x2=一2+x1<一2,∴g(一2)<0,即4a-2b+3<0,同理可求得
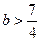 .
.故当0<x1<2时,
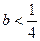 ;当一2<x1<0时,
;当一2<x1<0时,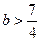 .
.本题涉及的变量较多,因此弄清问题的意义,确定变量并寻找变量间的关系就显
得特别重要。
(1)变量情况。
主要变量:限制在10秒和60秒之间的两次广告时间;
制约变量:总的费用≤36 000元,需影响年轻人数≥1500千人,需影响中年人数≥2 000
千人,需影响老年人数≥2000千人。
(2)变量间的关系:
总的费用=(购买的时间×每秒价格)之和;
影响的人数=(购买的时间×相应年龄组每秒影响的人数)之和;
销售额=(占影响人数的份额×对应组影响的人数)之和。
(3)建模与求解:记x、y分别表示早、晚购买的时间(秒);S=第一个月的销售额(用千人表示),C=总的费用(元);Y、M、O分别表示年轻、中年、老年组受到广告影响的人数(千人)。于是有:
C=400x+600y ≤3 600,
Y=30x+50y≥1500,
M=100x+80y≥2 000, (*)
O=50x+40y≥2 000,
10≤x≤60, 10≤y≤60
要求S=0.1Y+0.05M+0.02O=9x+9.8y的最大值。
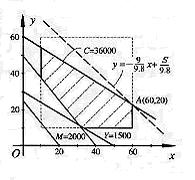
符合约束条件(*)的点(x,y)在如上图所示的六边形区域内,求S=9x+9.8y的最大值转化为求直线y=9x/9.8+S/9.8的截距S/9.8的最大值。由图知,当此直线过图中直线400x+600y=3600和x =60的交点A(60,20)时,截距最大,此时Smax=9×60+9.8×20=736(千人)。
(4) 结论:如上讨论可知,满意的结果是第一个月的销售额是736 000(份)只要购买晚八叫点前60秒和九点后20秒的广告即可。此时,花掉了所有的预算并超过所有年龄组所要求影响的人数。
得特别重要。
(1)变量情况。
主要变量:限制在10秒和60秒之间的两次广告时间;
制约变量:总的费用≤36 000元,需影响年轻人数≥1500千人,需影响中年人数≥2 000
千人,需影响老年人数≥2000千人。
(2)变量间的关系:
总的费用=(购买的时间×每秒价格)之和;
影响的人数=(购买的时间×相应年龄组每秒影响的人数)之和;
销售额=(占影响人数的份额×对应组影响的人数)之和。
(3)建模与求解:记x、y分别表示早、晚购买的时间(秒);S=第一个月的销售额(用千人表示),C=总的费用(元);Y、M、O分别表示年轻、中年、老年组受到广告影响的人数(千人)。于是有:
C=400x+600y ≤3 600,
Y=30x+50y≥1500,
M=100x+80y≥2 000, (*)
O=50x+40y≥2 000,
10≤x≤60, 10≤y≤60
要求S=0.1Y+0.05M+0.02O=9x+9.8y的最大值。

符合约束条件(*)的点(x,y)在如上图所示的六边形区域内,求S=9x+9.8y的最大值转化为求直线y=9x/9.8+S/9.8的截距S/9.8的最大值。由图知,当此直线过图中直线400x+600y=3600和x =60的交点A(60,20)时,截距最大,此时Smax=9×60+9.8×20=736(千人)。
(4) 结论:如上讨论可知,满意的结果是第一个月的销售额是736 000(份)只要购买晚八叫点前60秒和九点后20秒的广告即可。此时,花掉了所有的预算并超过所有年龄组所要求影响的人数。

练习册系列答案
相关题目
 的零点有( )
的零点有( ) 是函数
是函数 的一个零点,若
的一个零点,若 ,则
,则

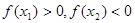

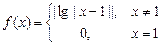 ,则关于
,则关于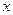 的方程
的方程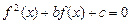 有7个不同实数解的充要条件是( )
有7个不同实数解的充要条件是( ) 且
且
 且
且

 且
且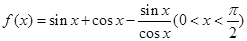 ,则函数
,则函数 的零点所在的区间为
的零点所在的区间为 



 ,若函数
,若函数 不存在零点,则c的取值范围是_________。
不存在零点,则c的取值范围是_________。 的定义域为
的定义域为 ,并满足以下三个条件:(i)对任意
,并满足以下三个条件:(i)对任意 ,有
,有 ;
; ,有
,有 ;(iii)
;(iii) 。
。 的值;
的值; ,且
,且 ,求证:
,求证: 。
。 满足
满足 ,当
,当 时,不等式
时,不等式 恒成立,则实数
恒成立,则实数 的范围为 ▲
的范围为 ▲