题目内容
已知二次函数f(x)=ax2+bx+c,(a<0)不等式f(x)>-2x的解集为(1,3).
(1)若方程f(x)+6a=0有两个相等的实根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求实数a的取值范围.
(1)若方程f(x)+6a=0有两个相等的实根,求f(x)的解析式;
(2)若f(x)的最大值为正数,求实数a的取值范围.
(1)∵不等式f(x)>-2x的解集为(1,3),
∴x=1和x=3是方程ax2+(b+2)x+c=0(a<0)的两根,
∴,∴b=-4a-2,c=3a,
又方程f(x)+6a=0有两个相等的实根.
∴Δ=b2-4a(c+6a)=0,∴4(2a+1)2-4a×9a=0.
∴(5a+1)(1-a)=0,∴a=-或a=1(舍).
∴a=-,b=-,c=-,
∴f(x)=-x2-x-.
(2)由(1)知f(x)=ax2-2(2a+1)x+3a
=a2-+3a
=a2+
∵a<0,
∴f(x)的最大值为,
∵f(x)的最大值为正数.
∴
∴解得a<-2-或-2+<a<0.
∴所求实数a的取值范围是∪(-2+,0).
∴x=1和x=3是方程ax2+(b+2)x+c=0(a<0)的两根,
∴,∴b=-4a-2,c=3a,
又方程f(x)+6a=0有两个相等的实根.
∴Δ=b2-4a(c+6a)=0,∴4(2a+1)2-4a×9a=0.
∴(5a+1)(1-a)=0,∴a=-或a=1(舍).
∴a=-,b=-,c=-,
∴f(x)=-x2-x-.
(2)由(1)知f(x)=ax2-2(2a+1)x+3a
=a2-+3a
=a2+
∵a<0,
∴f(x)的最大值为,
∵f(x)的最大值为正数.
∴
∴解得a<-2-或-2+<a<0.
∴所求实数a的取值范围是∪(-2+,0).
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中
中 、
、 异号,则函数的零点个数是( )
异号,则函数的零点个数是( )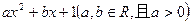 ,设方程f (x)
,设方程f (x)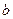 的取值范围.
的取值范围. +
+ =3的实数解的个数为( )
=3的实数解的个数为( )  对任意
对任意 都有
都有 且x>0时,
且x>0时, .(1)求
.(1)求 ,(其中
,(其中 )
) ,
, 的图象上有与
的图象上有与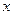 轴平行的切线,求
轴平行的切线,求 的取范围;
的取范围; 时取得极值,且
时取得极值,且 时,
时, 恒成立,求
恒成立,求 的取值范围。
的取值范围。 的图象所围成的图形的面积为
的图象所围成的图形的面积为 
 的实数解落在的区间是 ( )
的实数解落在的区间是 ( )


