Question

【题目】已知函数f（x）满足f（x+y）=f（x）f（y），且f（1）= ．
（1）当n∈N*时，求f（n）的表达式；
（2）设an=nf（n），n∈N* ， 求证a1+a2+a3+…+an＜2；
（3）设bn=（9﹣n） ，n∈N* ， Sn为bn的前n项和，当Sn最大时，求n的值．

Answer 1

【答案】
（1）解：令x=n．y=1，得到f（n+1）=f（n）f（1）= f（n），

所以{f（n）}是首项为 、公比为 的等比数列，即f（n）=

（2）解：∵ ， ，

，

两式相减得： ，

整理得

（3）解：∵f（n）= ，而bn=（9﹣n） ，n∈N*，则bn= ，

当n≤8时，bn＞0；当n=9时，bn=0；当n＞9时，bn＜0；

∴n=8或9时，Sn取到最大值

【解析】（1）由于函数f（x）满足f（x+y）=f（x）f（y）对任意的实数x，y都成立，故可令x=n，y=1，再由f（1）= 得到f（n）的表达式；（2）由（1）知，an=nf（n）= ，故可用错位相减法求出a1+a2+a3+…+an的表达式，即可得证；（3）由（1）和bn=（9﹣n） ，n∈N*可求bn的表达式，进而求出Sn ， 由于数列为一种特殊函数，故可利用函数单调性得到Sn最大时的n值．
【考点精析】本题主要考查了等比数列的通项公式（及其变式）和数列的前n项和的相关知识点，需要掌握通项公式：；数列{an}的前n项和sn与通项an的关系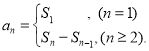才能正确解答此题．