��Ŀ����
����Ŀ��Ϊ�о����ΰ����Ƿ������йأ�����һ����ص��飬���в������ݶ�ʧ��������ȷ�����Dz���������������������ͬ�����̻��ΰ�����ռ������������![]() �������̵������У����ΰ��벻���ΰ��ı�Ϊ
�������̵������У����ΰ��벻���ΰ��ı�Ϊ![]() ��
��
��1�������̲����ΰ�����![]() �ˣ��ִӻ��ΰ��������÷ֲ�����ķ�����ȡ
�ˣ��ִӻ��ΰ��������÷ֲ�����ķ�����ȡ![]() �ˣ��ٴ���
�ˣ��ٴ���![]() ���������ȡ
���������ȡ![]() �˽��е��飬�������˶������̻��ΰ��ĸ��ʣ�
�˽��е��飬�������˶������̻��ΰ��ĸ��ʣ�
��2�����о��õ��ڷ�������ʲ�����![]() ��ǰ���£���Ϊ���ΰ��������йأ������̵����������ж��٣�
��ǰ���£���Ϊ���ΰ��������йأ������̵����������ж��٣�
���� 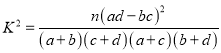 ������
������![]() ��
��
|
|
|
|
|
|
|
|
|
|
���𰸡���1��![]() ����2��������������Ϊ
����2��������������Ϊ![]() �ˣ�
�ˣ�
�������������������1����������̵�����![]() �ˣ��������ɵ����зΰ�����16�ˣ������ΰ�����4�ˣ����ֲ�����Ķ���ɵó�ȡ��5���У�4�˻�����1�˲������������оٷ��ɵó�ȡ��ʽ����10�֣���������6�֣��ɸ��ʼ��㹫ʽ�ɵý������2������������Ϊ
�ˣ��������ɵ����зΰ�����16�ˣ������ΰ�����4�ˣ����ֲ�����Ķ���ɵó�ȡ��5���У�4�˻�����1�˲������������оٷ��ɵó�ȡ��ʽ����10�֣���������6�֣��ɸ��ʼ��㹫ʽ�ɵý������2������������Ϊ![]() ���г�
���г�![]() ���������ɱ������
���������ɱ������![]() �����ݱ���
�����ݱ���![]() �����
�����![]() ���ɵ������.
���ɵ������.
�����������1������������Ϊ![]() ����������
����������![]() ���������̵�����
���������̵�����![]() �ˣ��������̻��ΰ�����16�ˣ������ΰ�����4�ˣ��÷ֲ�����ķ�����ȡ5�ˣ���Ӧ��ȡ���̻��ΰ���4�ˣ���Ϊ
�ˣ��������̻��ΰ�����16�ˣ������ΰ�����4�ˣ��÷ֲ�����ķ�����ȡ5�ˣ���Ӧ��ȡ���̻��ΰ���4�ˣ���Ϊ![]() �������̻��ΰ���1�ˣ���ΪA����5���������ȡ2�ˣ����п��ܵĽ����
�������̻��ΰ���1�ˣ���ΪA����5���������ȡ2�ˣ����п��ܵĽ����![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����
����![]() �֣��������˶������̻��ΰ������ι���
�֣��������˶������̻��ΰ������ι���![]() �֣���
�֣���![]() ���������˶������̻��ΰ��ĸ���Ϊ
���������˶������̻��ΰ��ĸ���Ϊ![]() ��
��
��2������������Ϊ![]() ��������ɵ����������£�
��������ɵ����������£�
���ΰ� | �����ΰ� | �ϼ� | |
���� |
|
|
|
������ |
|
|
|
�ܼ� |
|
|
|
�ɱ��ã�  ��������
��������![]() ����
����![]() ��
��
��![]() ��������
Ϊ��������![]() ����СֵΪ
����СֵΪ![]() ����
����![]() ����������������Ϊ
����������������Ϊ![]() �ˣ�
�ˣ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�