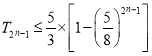题目内容

【题目】已知单调递减的等比数列{an}满足：a2+a3+a4=28，且a3+2是a2 ， a4是等差中项，则公比q= ， 通项公式为an= ．

【答案】；26﹣n
【解析】解：设单调递减的等比数列{an}的公比为q，
∵a2+a3+a4=28，且a3+2是a2 ， a4是等差中项，
∴ =28，2（a3+2）=a2+a4 ， 即2（a3+2）= +a3q，
解得a3=8，q= ，（q=2舍去）．
∴an= =8× =26﹣n ．
故答案分别为： ；26﹣n ．
【考点精析】根据题目的已知条件，利用等比数列的通项公式（及其变式）和等比数列的前n项和公式的相关知识可以得到问题的答案，需要掌握通项公式：；前项和公式：．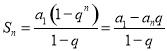

练习册系列答案
相关题目

【题目】已知函数f（x）满足f（x+y）=f（x）f（y），且f（1）= ．
（1）当n∈N*时，求f（n）的表达式；
（2）设an=nf（n），n∈N* ， 求证a1+a2+a3+…+an＜2；
（3）设bn=（9﹣n） ，n∈N* ， Sn为bn的前n项和，当Sn最大时，求n的值．

【题目】将函数f（x）=cos（ωx+φ）（ω＞0，|φ|＜ ）的图象上的每一点的纵坐标不变，横坐标缩短为原来的一半，再将图象向右平移 个单位长度得到函数y=sinx的图象．
（1）直接写出f（x）的表达式，并求出f（x）在[0，π]上的值域；
（2）求出f（x）在[0，π]上的单调区间．

【题目】已知曲线： ， ： （），从上的点作轴的垂线，交于点，再从点作轴的垂线，交于点.设， ， .

（Ⅰ）求数列的通项公式；

（Ⅱ）记，数列的前项和为，求证： ；

（Ⅲ）若已知（），记数列的前项和为，数列的前项和为，试比较与的大小.

【题目】我国是世界上严重缺水的国家之一，城市缺水问题较为突出．某市为了节约生活用水，计划在本市试行居民生活用水定额管理（即确定一个居民月均用水量标准用水量不超过a的部分按照平价收费，超过a的部分按照议价收费）．为了较为合理地确定出这个标准，通过抽样获得了 100位居民某年的月均用水量（单位：t），制作了频率分布直方图．

（1）由于某种原因频率分布直方图部分数据丢失，请在图中将其补充完整；
（2）用样本估计总体，如果希望80%的居民每月的用水量不超出标准则月均用水量的最低标准定为多少吨，请说明理由；
（3）从频率分布直方图中估计该100位居民月均用水量的众数，中位数，平均数（同一组中的数据用该区间的中点值代表）．

【题目】如图，在四棱锥P﹣ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．
（Ⅰ）证明：CD⊥AE；
（Ⅱ）证明：PD⊥平面ABE；
（Ⅲ）求二面角A﹣PD﹣C的正切值．

【题目】正方形ABCD一条边AB所在方程为x+3y﹣5=0，另一边CD所在直线方程为x+3y+7=0，
（Ⅰ）求正方形中心G所在的直线方程；
（Ⅱ）设正方形中心G（x0 ， y0），当正方形仅有两个顶点在第一象限时，求x0的取值范围．

【题目】如图所示，在△ABC中，B= ，AC=2 ，cosC= ．

（1）求sin∠BAC的值及BC的长度；
（2）设BC的中点为D，求中线AD的长．

【题目】用0、1、2、3、4这五个数字，可以组成多少个满足下列条件的没有重复数字的五位数？
（1）奇数；
（2）比21034大的偶数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网