Question

【题目】设函数f（x）=2sin（2x+φ）（0＜φ＜π），y=f（x）图象的一个对称中心是 ．

（1）求φ；
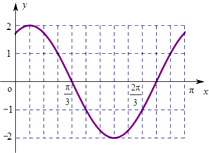
（2）在给定的平面直角坐标系中作出该函数在x∈[0，π]的图象；
（3）求函数f（x）≥1（x∈R）的解集．

Answer 1

【答案】
（1）解：∵ 是函数y=f（x）的图象的对称中心，

∴ ，∴ ，

∴ ∵0＜φ＜π，∴ ，

即 ．

（2）解：列表

x	0					π
			π		2π
f（x）		2	0	﹣2	0

（3）解：∵f（x）≥1，

即 ， ．

∴ ，

求函数f（x）≥1（x∈R）的解集是 ．

【解析】（1）根据函数的对称中心代入即可求φ；（2）利用五点法即可在给定的平面直角坐标系中作出该函数在x∈[0，π]的图象；（3）结合三角不等式进行求解即可．
【考点精析】解答此题的关键在于理解五点法作函数y=Asin（ωx+φ）的图象的相关知识，掌握描点法及其特例—五点作图法（正、余弦曲线），三点二线作图法（正、余切曲线）．