题目内容
已知
=2，则tanα的值为 ．
| sinα+cosα |
| 2sinα-cosα |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：利用三角函数的基本关系式，将等式的左边分子分母分别除以cosα，然后解方程即可．
解答：
解：由已知，将左边分子分母分别除以cosα，得
=2，解得tanα=1；
故答案为：1．
| tanα+1 |
| 2tanα-1 |
故答案为：1．
点评：本题考查了三角函数的基本关系式中商数关系的运用，属于基础题．
练习册系列答案
相关题目
若圆x2+y2+mx-
=0与直线y=-1相切，且其圆心在y轴的左侧，则m的值为（ ）
| 1 |
| 4 |
| A、0 | ||
| B、2 | ||
| C、1 | ||
D、
|
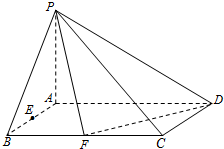已知在四棱锥P-ABCD中，底面ABCD是矩形，且AD=2，AB=1，PA⊥平面ABCD，E、F分别是线段AB、BC的中点．椭圆
（θ为参数）的离心率为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|