题目内容
已知f(x)=ax2+bx+c,且b>0,若对任意x有f(x)≥0,则
的最小值为( )
| f(1) |
| b |
| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
考点:二次函数的性质
专题:函数的性质及应用
分析:由二次函数f(x)对于任意实数x都有f(x)≥0,得到二次函数的开口方向和最小值,从而确定a,b,c的关系.
解答:
解:因为二次函数f(x)=ax2+bx+c对于任意实数x都有f(x)≥0.
则图象开口向上,且△≤0,联立有
则4ac≥b2≥0,所以c>0且ac≥
,即
≥
,
所以
=
=
+
+1,
∵b>0,a>0,c>0,
∴
>0,
>0,
∴
≥2
+1≥2
+1=2,(当且仅当a=c时成立)
所以
的最小值为2.
则图象开口向上,且△≤0,联立有
|
则4ac≥b2≥0,所以c>0且ac≥
| b2 |
| 4 |
| ac |
| b2 |
| 1 |
| 4 |
所以
| f(1) |
| b |
| a+b+c |
| b |
| a |
| b |
| c |
| b |
∵b>0,a>0,c>0,
∴
| a |
| b |
| c |
| b |
∴
| f(1) |
| b |
|
|
所以
| f(1) |
| b |
点评:本题考查了二次函数的图象和性质,以及基本不等式的应用.

练习册系列答案
相关题目
双曲线
-
=1(a>0,b>0)的离心率是2,则渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、3x±y=0 | ||
B、x±
| ||
| C、x±3y=0 | ||
D、
|
某班对期中考试成绩优秀的学生进行奖励,全班共有5人获奖,其中有2个来自A学习小组,2人来自B学习小组,1人来自C学习小组,现让这5人排成一排合影,要求同学习小组的同学不能相邻,那么不同的排法共有 种.
椭圆
(θ为参数)的离心率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
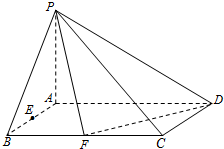 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.