题目内容
在正四棱柱ABCD-A1B1C1D1中,AA1=2,AB=BC=1,动点P,Q分别在线段C1D,AC上,则线段PQ长度的最小值是 .
考点:点、线、面间的距离计算
专题:计算题,空间位置关系与距离
分析:建立空间直角坐标系,设点P的坐标为(0,λ,2λ),λ∈[0,1],点Q的坐标为(1-μ,μ,0),μ∈[0,1],求出PQ,利用配方法,即可求出线段PQ长度的最小值.
解答:
 解:建立如图所示的空间直角坐标系,则A(1,0,0),B(1,1,0),C(0,1,0),C1(0,1,2),
解:建立如图所示的空间直角坐标系,则A(1,0,0),B(1,1,0),C(0,1,0),C1(0,1,2),
设点P的坐标为(0,λ,2λ),λ∈[0,1],点Q的坐标为(1-μ,μ,0),μ∈[0,1],
∴PQ=
,
当且仅当λ=
,μ=
时,线段PQ的长度取得最小值
.
故答案为:
.
 解:建立如图所示的空间直角坐标系,则A(1,0,0),B(1,1,0),C(0,1,0),C1(0,1,2),
解:建立如图所示的空间直角坐标系,则A(1,0,0),B(1,1,0),C(0,1,0),C1(0,1,2),设点P的坐标为(0,λ,2λ),λ∈[0,1],点Q的坐标为(1-μ,μ,0),μ∈[0,1],
∴PQ=
5(λ-
|
当且仅当λ=
| 1 |
| 9 |
| 5 |
| 9 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题考查求线段PQ长度的最小值,考查向量法的运用,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
数列{an}的通项公式an=
,若{an}的前n项和为24,则n为( )
| 1 | ||||
|
| A、25 | B、576 |
| C、624 | D、625 |
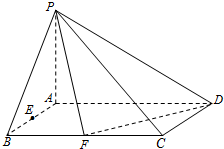 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.