题目内容
16.已知集合A={y|y=x2,x∈[-1,3]},B={y|y=4x,x∈[-1,3]},C={(x,y)|y=x2,x∈[-1,3]},D={(x,y)|y=4x,x∈[-1,3]}.A与B的关系是A⊆B;C与D的关系是C∩D=∅.分析 分别化简集合,理解集合的含义,即可得出结论.
解答 解:集合A={y|y=x2,x∈[-1,3]}=[0,9],B={y|y=4x,x∈[-1,3]}=[-4,12],
∴A⊆B;
C={(x,y)|y=x2,x∈[-1,3]}表示二次函数上的点的集合;D={(x,y)|y=4x,x∈[-1,3]}表示线段上的点的集合,
∴C∩D=∅.
故答案为:A⊆B;C∩D=∅.
点评 本题考查集合的含义,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
8.设函数f(x)=$\sqrt{a{x}^{2}+bx}$(b>0,a<0)的定义域与值域相等,则a的值等于( )
| A. | -4 | B. | -2 | C. | -8 | D. | -6 |
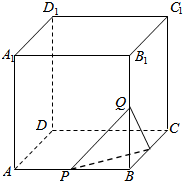 如图所示,P、Q、R分别是正方形的棱AB、BB1、BC的中点,则BD1与平面PQR的位置关系是BD1⊥平面PQR.
如图所示,P、Q、R分别是正方形的棱AB、BB1、BC的中点,则BD1与平面PQR的位置关系是BD1⊥平面PQR.