题目内容
6．
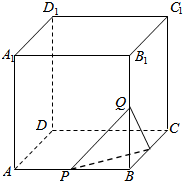如图所示，P、Q、R分别是正方形的棱AB、BB1、BC的中点，则BD1与平面PQR的位置关系是BD1⊥平面PQR．
分析 连接BC1，根据直线与平面垂直的判定定理可知只需证BD1与平面MNP内两相交直线垂直，而BD1⊥PM，而BD1⊥MN，MN∩PM=M，进而得到BD1⊥平面MNP．
解答 解：连接BC1，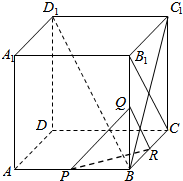
由正方体的性质得BC1是BD1在平面BCC1B1内的射影，且B1C⊥BC1，
∴BD1⊥B1C，
∵R为BC的中点，P为AB的中点，Q为BB1的中点．
∴B1C∥QR，
∴BD1⊥QR，
同理BD1⊥RP
又RP∩QR=R，
∴BD1⊥平面PQR．
故答案为：BD1⊥平面PQR
点评 本题主要考查了直线与平面垂直的判定，考查空间想象能力和推理论证能力，属于基础题．
练习册系列答案
相关题目
1．已知公比为q（q≠1），的等比数列{an}的前n项和为Sn，则数列{$\frac{1}{{a}_{n}}$}的前n项和为（ ）
| A． | $\frac{{q}^{n}}{{S}_{n}}$ | B． | $\frac{{S}_{n}}{{q}^{n}}$ | C． | $\frac{1}{{S}_{n}{q}^{n-1}}$ | D． | $\frac{{S}_{n}}{{a}_{{1}^{2}}{q}^{n-1}}$ |