题目内容
已知f(x)是定义在R上的奇函数,若对于x≥0,都有f(x+2)=f(x),且当x∈[0,2]时,f(x)=ex-1,则f(2 013)+f(-2 014)=( ).
| A.1-e | B.e-1 |
| C.-1-e | D.e+1 |
B
由f(x+2)=f(x)可知函数的周期是2,
所以f(2 013)=f(1)=e-1,f(-2 014)=-f(2 014)=-f(0)=0,
所以f(2 013)+f(-2 014)=e-1.
所以f(2 013)=f(1)=e-1,f(-2 014)=-f(2 014)=-f(0)=0,
所以f(2 013)+f(-2 014)=e-1.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
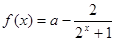 ,其中
,其中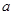 为常数
为常数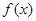 为奇函数,试确定
为奇函数,试确定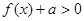 恒成立,求实数
恒成立,求实数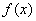 是定义在实数集
是定义在实数集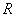 上的以2为周期的偶函数,当
上的以2为周期的偶函数,当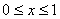 时,
时,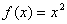 .若直线
.若直线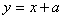 与函数
与函数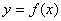 的图像在
的图像在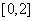 内恰有两个不同的公共点,则实数
内恰有两个不同的公共点,则实数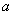 的值是( )
的值是( ) 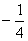 或
或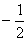 ;
;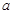 为实常数,
为实常数,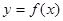 是定义在
是定义在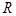 上的奇函数,且当
上的奇函数,且当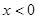 时,
时,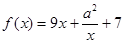 .
.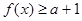 对一切
对一切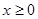 成立,则
成立,则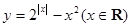 的图象大致为( )
的图象大致为( )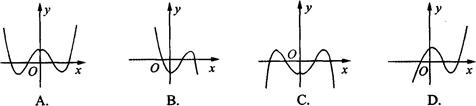
 ,其中
,其中 为已知实数,
为已知实数, ,则下列各命题中错误的是( )
,则下列各命题中错误的是( )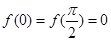 ,则
,则 对任意实数恒成立;
对任意实数恒成立; ,则函数
,则函数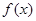 为奇函数;
为奇函数; ,则函数
,则函数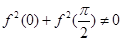 时,若
时,若 ,则
,则