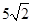题目内容
已知等比数列{an}的前n项和Sn满足:S4-S1=28,且a3+2是a2,a4的等差中项.
(1)求数列{an}的通项公式;
(2)若数列{an}为递增数列,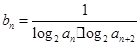 ,
,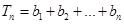 ,问是否存在最小正整数n使得
,问是否存在最小正整数n使得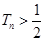 成立?若存在,试确定n的值,不存在说明理由.
成立?若存在,试确定n的值,不存在说明理由.
(1)求数列{an}的通项公式;
(2)若数列{an}为递增数列,
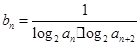 ,
,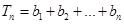 ,问是否存在最小正整数n使得
,问是否存在最小正整数n使得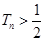 成立?若存在,试确定n的值,不存在说明理由.
成立?若存在,试确定n的值,不存在说明理由.(1)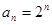 或
或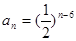 ;(2)
;(2)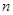 的最小值为
的最小值为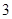 .
.
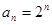 或
或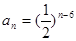 ;(2)
;(2)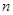 的最小值为
的最小值为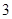 .
. 试题分析:(1)由已知可得
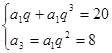 ,解之得
,解之得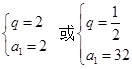 ,
,从而可得
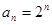 或
或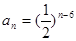 .
.(2)根据数列
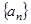 单调递增,得
单调递增,得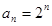 ,从而
,从而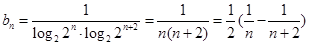 ,
, 利用“裂项相消法”求得
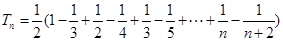 =
=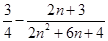 .
. 假设存在,根据
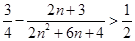 ,解得
,解得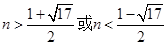 (不合题意舍去),
(不合题意舍去),依据
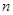 为正整数,所以
为正整数,所以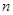 的最小值为
的最小值为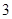 .
. (1)设等比数列
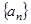 的首项为
的首项为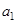 ,公比为q,
,公比为q,依题意,有
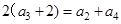 ,
,由
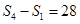 可得
可得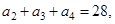 得
得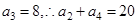 3分
3分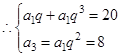 解之得
解之得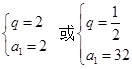 5分
5分所以
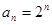 或
或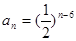 6分
6分(2)因为数列
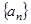 单调递增,
单调递增,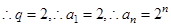
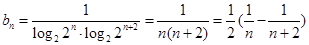 , 7分
, 7分所以
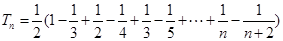
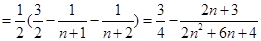 . 9分
. 9分假设存在,则有
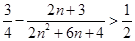 ,整理得:
,整理得: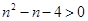
解得
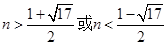 (不合题意舍去) 11分
(不合题意舍去) 11分又因为
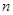 为正整数,所以
为正整数,所以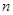 的最小值为
的最小值为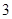 . 12分
. 12分
练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
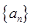 中,
中,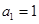 ,前
,前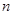 项的和是
项的和是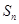 ,且
,且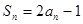 ,
,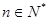 .
.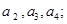
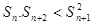 .
.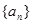 的前
的前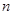 项和为
项和为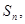 满足
满足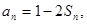 (
( 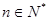 )
)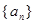 为等比数列;
为等比数列;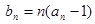 ,求数列
,求数列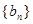 的前
的前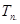
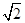 ,则2a7+a11的最小值为( )
,则2a7+a11的最小值为( )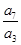 =( )
=( )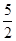
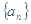 是公比为2的等比数列,若
是公比为2的等比数列,若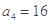 ,则
,则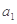 = ( )
= ( )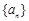 中,
中,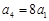 ,则公比
,则公比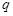 的值为
的值为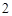

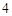
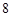
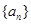 是等比数列,
是等比数列,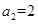 ,
,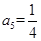 ,则公比
,则公比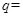 ______________.
______________. 中,
中,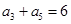 ,
,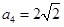 ,则
,则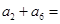 ( )
( )