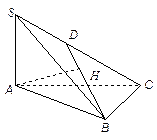题目内容
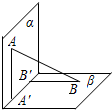
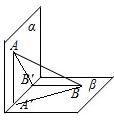
如图,平面α⊥平面β,A∈α,B∈β,AB与平面α所成的角为
,过A、B分别作两平面交线的垂线,垂足为A′、B′,若AB=3A'B',则AB与平面β所成的角的正弦值是( )
| π |
| 4 |
A.
| B.
| C.
| D.
|

连接AB‘,BA’,
∵平面α⊥平面β,A∈α,B∈β,AB与平面α所成的角为
,
过A、B分别作两平面交线的垂线,垂足为A′、B′,
∴∠B′AB=
,AA′⊥β,BB′⊥α,∠ABA′是AB与平面β所成的角,
设A′B′=a,∵AB=3A'B',∴AB=3a,
设AB′=BB′=x,则2x2=9a2,解得AB′=BB′=
a,
∴A′B=
=
a,AA′=
=
a,
∴sin∠ABA′=
=
.
故选A.
∵平面α⊥平面β,A∈α,B∈β,AB与平面α所成的角为
| π |
| 4 |
过A、B分别作两平面交线的垂线,垂足为A′、B′,
∴∠B′AB=
| π |
| 4 |
设A′B′=a,∵AB=3A'B',∴AB=3a,
设AB′=BB′=x,则2x2=9a2,解得AB′=BB′=
3
| ||
| 2 |
∴A′B=
|
| ||
| 2 |
9a2-
|
| ||
| 2 |
∴sin∠ABA′=
| ||||
| 3a |
| ||
| 6 |
故选A.


练习册系列答案
相关题目
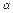 ∥平面
∥平面 ,点A∈
,点A∈ 线段AB,CD上,且AE∶EB=CF∶FD.
线段AB,CD上,且AE∶EB=CF∶FD.