题目内容
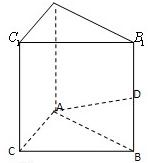
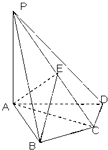
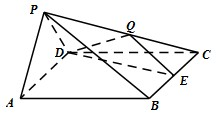
四棱锥P-ABCD中,底面ABCD是边长为2的菱形,侧面PAD⊥底面ABCD,∠BCD=60°,PA=PD=
,E是BC中点,点Q在侧棱PC上.
(Ⅰ)求证:AD⊥PB;
(Ⅱ)若Q是PC中点,求二面角E-DQ-C的余弦值;
(Ⅲ)若
=λ,当PA∥平面DEQ时,求λ的值.
| 2 |
(Ⅰ)求证:AD⊥PB;
(Ⅱ)若Q是PC中点,求二面角E-DQ-C的余弦值;
(Ⅲ)若
| PQ |
| PC |

(Ⅰ)证明:取AD中点O,连接OP,OB,BD.
因为PA=PD,所以PO⊥AD.…(1分)
因为菱形ABCD中,∠BCD=60°,所以AB=BD,所以BO⊥AD.…(2分)
因为BO∩PO=O,所以AD⊥平面POB,所以AD⊥PB.…(5分)
(Ⅱ)由(Ⅰ)知BO⊥AD,PO⊥AD.
因为侧面PAD⊥底面ABCD,且平面PAD∩底面ABCD=AD,所以PO⊥底面ABCD.…(6分)
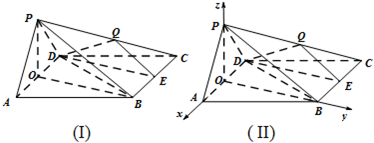
以O为坐标原点,如图建立空间直角坐标系O-xyz.…(7分)
则D(-1,0,0),E(-1,
,0),P(0,0,1),C(-2,
,0),
因为Q为PC中点,所以Q(-1,
,
).…(8分)
所以
=(0,
,0),
=(0,
,
),所以平面DEQ的法向量为
=(1,0,0).
因为
=(-1,
,0),
=(0,
,
),
设平面DQC的法向量为
=(x,y,z),则
,∴
令x=
,则y=1,z=-
,即
=(
,1,-
).…(9分)cos<
,
>=
=
.
由图可知,二面角E-DQ-C为锐角,所以余弦值为
.…(10分)
(Ⅲ)因为
=λ,所以
=λ
,
由(Ⅱ)知
=(-2,
,-1),
=(1,0,-1),
若设Q(x,y,z),则
=(x,y,z-1),
由
=λ
,得
,
在平面DEQ中,
=(0,
,0),
=(x+1,y,z)=(1-2λ,
λ,1-λ),
所以平面DEQ法向量为
=(1-λ,0,2λ-1),…(12分)
又因为PA∥平面DEQ,所以
•
=0,…(13分)
即(1-λ)+(-1)(2λ-1)=0,得λ=
.
所以,当λ=
时,PA∥平面DEQ.…(14分)
因为PA=PD,所以PO⊥AD.…(1分)
因为菱形ABCD中,∠BCD=60°,所以AB=BD,所以BO⊥AD.…(2分)
因为BO∩PO=O,所以AD⊥平面POB,所以AD⊥PB.…(5分)
(Ⅱ)由(Ⅰ)知BO⊥AD,PO⊥AD.
因为侧面PAD⊥底面ABCD,且平面PAD∩底面ABCD=AD,所以PO⊥底面ABCD.…(6分)
以O为坐标原点,如图建立空间直角坐标系O-xyz.…(7分)
则D(-1,0,0),E(-1,
| 3 |
| 3 |
因为Q为PC中点,所以Q(-1,
| ||
| 2 |
| 1 |
| 2 |
所以
| DE |
| 3 |
| DQ |
| ||
| 2 |
| 1 |
| 2 |
| n1 |
因为
| DC |
| 3 |
| DQ |
| ||
| 2 |
| 1 |
| 2 |
设平面DQC的法向量为
| n2 |
|
|
令x=
| 3 |
| 3 |
| n2 |
| 3 |
| 3 |
| n1 |
| n2 |
| ||||
|
|
| ||
| 7 |
由图可知,二面角E-DQ-C为锐角,所以余弦值为
| ||
| 7 |
(Ⅲ)因为
| PQ |
| PC |
| PQ |
| PC |
由(Ⅱ)知
| PC |
| 3 |
| PA |
若设Q(x,y,z),则
| PQ |
由
| PQ |
| PC |
|
在平面DEQ中,
| DE |
| 3 |
| DQ |
| 3 |
所以平面DEQ法向量为
| n1 |
又因为PA∥平面DEQ,所以
| PA |
| n1 |
即(1-λ)+(-1)(2λ-1)=0,得λ=
| 2 |
| 3 |
所以,当λ=
| 2 |
| 3 |


练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目