题目内容

3．用三段论推理：“对数函数y=logax（a＞0且a≠1）在（0，+∞）上是减函数，因为y=log2x是对数函数，所以y=log2x在（0，+∞）上是减函数”，你认为这个推理（　　）
A．大前提错误B．小前提错误
C．推理形式错误D．大前提和小前提都错误

分析 当a＞1时，对数函数y=logax在（0，+∞）上是增函数，当0＜a＜1时，对数函数y=logax在（0，+∞）上是减函数，故可得结论．

解答 解：当a＞1时，对数函数y=logax在（0，+∞）上是增函数，
当0＜a＜1时，对数函数y=logax在（0，+∞）上是减函数，
故推理的大前提是错误的
故选：A

点评 本题考查演绎推理，考查三段论，考查对数函数的图象和性质，属于基础题．

练习册系列答案
相关题目
13．设l，m是两条不同的直线，α，β是两个不重合的平面，给出下列四个命题：
①若α∥β，l⊥α，则l⊥β；  ②若l∥m，l?α，m?β，则α∥β；
③若m⊥α，l⊥m，则l∥α；  ④若α⊥β，l?α，m?β，则l⊥m．
其中真命题的序号为①．
14．某机构对儿童记忆能力x和识图能力y进行统计分析，得到如下数据：
记忆能力x46810
识图能力y3568
由表中数据，求得线性回归方程为$\stackrel{∧}{y}$=$\frac{4}{5}$$\stackrel{∧}{x}$+$\stackrel{∧}{a}$（$\hat a=\overline y-\frac{4}{5}$$\overline x$），若某儿童记忆能力为12，则他识图能力为（　　）
A．9.2B．9.8C．9.5D．10
11．如图，已知A（10，0），直线x=t（0＜t＜10）与函数y=ex的图象交于点P，与x轴交于点H，记△APH的面积为f（t）．
（1）求函数f（t）的解析式；
（2）求函数f（t）的最大值．
（3）若g（t）=$\left\{{\begin{array}{l}{f（t）•{e^{-t}}+\frac{1}{6}{t^3}-4（{t＞0}）}\\{bt（{t≤0}）}\end{array}}$
探究：是否存在实数m，使得方程g（t）=m有且只有三个实数解，若存在求出m的取值范围，若不存在，请说明理由．
18．已知△ABC的三个顶点的直角坐标分别为A（2，-1），B（0，0），C（2+m，-2），且∠BAC为钝角，则实数m的取值范围为（-$\frac{1}{2}$，2）∪（2，+∞）．
8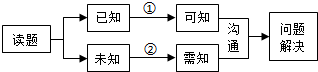．如图是解决数学问题的思维过程的流程图：图中①、②两条流程线与“推理与证明”中的思维方法相匹配是（　　）
A．①-分析法，②-综合法B．①-综合法，②-分析法
C．①-综合法，②-反证法D．①-分析法，②-反证法
15．sin120°=（　　）
A．-$\frac{1}{2}$B．$\frac{1}{2}$C．-$\frac{\sqrt{3}}{2}$D．$\frac{\sqrt{3}}{2}$
3．设复数z1=1-3i，z2=3+2i，则z1+z2在复平面内对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
4．设f0（x）=sinx，f1（x）=f${\;}_{0}^{′}$（x），f2（x）=f${\;}_{1}^{′}$（x），…，fn+1（x）=f${\;}_{n}^{′}$（x），n∈N，则f2015（x）=-cosx．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网