题目内容
4.设f0(x)=sinx,f1(x)=f${\;}_{0}^{′}$(x),f2(x)=f${\;}_{1}^{′}$(x),…,fn+1(x)=f${\;}_{n}^{′}$(x),n∈N,则f2015(x)=-cosx.分析 通过题意计算出f1(x)、f2(x)、f3(x)、f4(x)的值,利用其周期性即得结论.
解答 解:∵f0(x)=sinx,
∴f1(x)=f${\;}_{0}^{′}$(x)=cosx,
f2(x)=f${\;}_{1}^{′}$(x)=-sinx,
f3(x)=${f}_{2}^{′}$(x)=-cosx,
f4(x)=${f}_{3}^{′}$(x)=sinx,
…
∵2015=503×4+3,
∴f2015(x)=f3(x)=-cosx,
故答案为:-cosx.
点评 本题考查函数的周期性及求导,注意解题方法的积累,属于中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
3.用三段论推理:“对数函数y=logax(a>0且a≠1)在(0,+∞)上是减函数,因为y=log2x是对数函数,所以y=log2x在(0,+∞)上是减函数”,你认为这个推理( )
| A. | 大前提错误 | B. | 小前提错误 | ||
| C. | 推理形式错误 | D. | 大前提和小前提都错误 |
12.复平面上有点A,B其对应的复数分别为-3+i和-1-3i,O为原点,那么△AOB是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等腰直角三角形 | D. | 正三角形 |
13.已知f1(x)=sinx,f2(x)=f1′(x),f3(x)=f2′(x),f4(x)=f3′(x),…,fn(x)=fn-1′(x),则f2015(x)等于( )
| A. | cosx | B. | -cosx | C. | sinx | D. | -sinx |
14.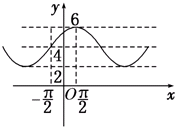 已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
 已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
已知函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )| A. | y=2cos($\frac{x}{2}$-$\frac{π}{4}$)+4 | B. | y=2cos($\frac{x}{2}$+$\frac{π}{4}$)+4 | C. | y=4cos($\frac{x}{2}$-$\frac{π}{4}$)+2 | D. | y=4cos($\frac{x}{2}$+$\frac{π}{4}$)+2 |