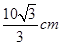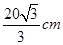题目内容
已知函数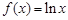 ,
,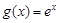 .
.
(Ⅰ)若函数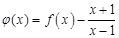 ,求函数
,求函数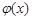 的单调区间;
的单调区间;
(Ⅱ)设直线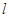 为函数
为函数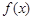 的图象上一点
的图象上一点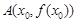 处的切线.证明:在区间
处的切线.证明:在区间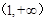 上存在唯一的
上存在唯一的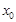 ,使得直线
,使得直线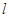 与曲线
与曲线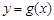 相切.
相切.
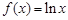 ,
,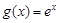 .
.(Ⅰ)若函数
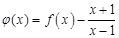 ,求函数
,求函数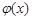 的单调区间;
的单调区间; (Ⅱ)设直线
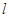 为函数
为函数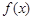 的图象上一点
的图象上一点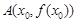 处的切线.证明:在区间
处的切线.证明:在区间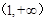 上存在唯一的
上存在唯一的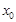 ,使得直线
,使得直线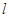 与曲线
与曲线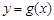 相切.
相切.(1)单调递增区间为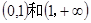
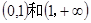
:(Ⅰ)求导,由导数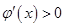 可求得增区间,(Ⅱ)先写出切线方程,证明唯一。
可求得增区间,(Ⅱ)先写出切线方程,证明唯一。
解:(Ⅰ)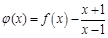
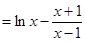 ,
,
 . ……………………2分
. ……………………2分
∵ 且
且 ,
,
∴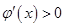 ,
,
∴函数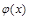 的单调递增区间为
的单调递增区间为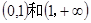 . ……………………4分
. ……………………4分
(Ⅱ)∵ ,∴
,∴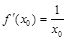 ,
,
∴ 切线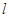 的方程为
的方程为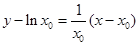 ,
,
即 , ① ……………………6分
, ① ……………………6分
设直线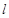 与曲线
与曲线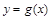 相切于点
相切于点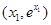 ,
,
∵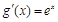 ,∴
,∴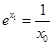 ,∴
,∴ . ……………………8分
. ……………………8分
∴直线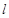 的方程为
的方程为 ,
,
即 , ② ……………………9分
, ② ……………………9分
由①②得 ,
,
∴ . …………………11分
. …………………11分
下证:在区间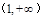 上
上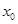 存在且唯一:
存在且唯一:
由(Ⅰ)可知,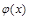
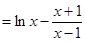 在在区间
在在区间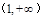 上递增.
上递增.
又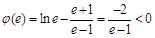 ,
,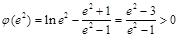 , ……………13分
, ……………13分
结合零点存在性定理,说明方程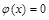 必在区间
必在区间 上有唯一的根,这个根就是所求的唯一
上有唯一的根,这个根就是所求的唯一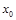 .
.
故结论成立. ………………14分
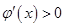 可求得增区间,(Ⅱ)先写出切线方程,证明唯一。
可求得增区间,(Ⅱ)先写出切线方程,证明唯一。解:(Ⅰ)
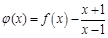
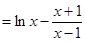 ,
, . ……………………2分
. ……………………2分∵
 且
且 ,
,∴
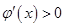 ,
,∴函数
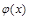 的单调递增区间为
的单调递增区间为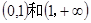 . ……………………4分
. ……………………4分(Ⅱ)∵
 ,∴
,∴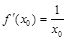 ,
,∴ 切线
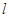 的方程为
的方程为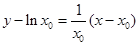 ,
,即
 , ① ……………………6分
, ① ……………………6分设直线
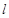 与曲线
与曲线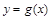 相切于点
相切于点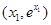 ,
,∵
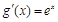 ,∴
,∴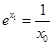 ,∴
,∴ . ……………………8分
. ……………………8分∴直线
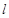 的方程为
的方程为 ,
,即
 , ② ……………………9分
, ② ……………………9分由①②得
 ,
,∴
 . …………………11分
. …………………11分下证:在区间
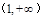 上
上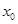 存在且唯一:
存在且唯一:由(Ⅰ)可知,
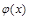
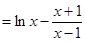 在在区间
在在区间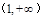 上递增.
上递增.又
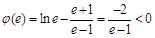 ,
,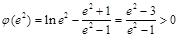 , ……………13分
, ……………13分结合零点存在性定理,说明方程
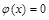 必在区间
必在区间 上有唯一的根,这个根就是所求的唯一
上有唯一的根,这个根就是所求的唯一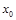 .
. 故结论成立. ………………14分

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
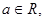 函数
函数 。
。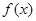 在区间
在区间 上最小值
上最小值 ;
;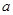 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数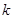 的取值范围;
的取值范围;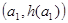 ,B
,B ,C
,C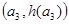 ,从左到右依次是函数
,从左到右依次是函数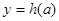 图象上三点,且这三点不共线,求证:
图象上三点,且这三点不共线,求证: 是钝角三角形。
是钝角三角形。 (
(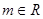 ),
),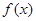 的导数为
的导数为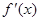 ,且
,且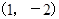
 ,若
,若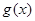 在
在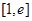 的最小值是2,求实数
的最小值是2,求实数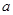 的值.
的值.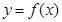 满足:当
满足:当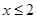 时,
时,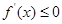 ;当
;当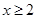 时,
时,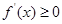 .则下列结论:①
.则下列结论:①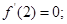 ②
②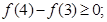 ③
③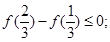 ④
④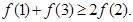 其中成立的个数是( )
其中成立的个数是( )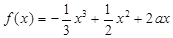 在区间
在区间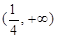 上存在单调递增区间,则的取值范围是
上存在单调递增区间,则的取值范围是 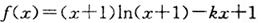 ,,k为常数,e是自然对数的底数).
,,k为常数,e是自然对数的底数).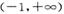 上的图象均在第一、二象限?若存在,求出k的最大值;若不存在,请说明理由;
上的图象均在第一、二象限?若存在,求出k的最大值;若不存在,请说明理由;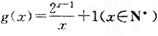 ,记
,记 ,求证:
,求证: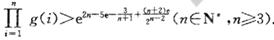
 )内是增函数,则实数a的取值范围是( )
)内是增函数,则实数a的取值范围是( ) 3;
3; 3
3
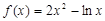 的单调递增区间是 。
的单调递增区间是 。 ,要使其体积为最大,则高为( )
,要使其体积为最大,则高为( )