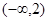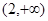题目内容
已知定义在R 上的可导函数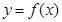 满足:当
满足:当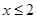 时,
时,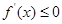 ;当
;当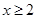 时,
时,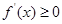 .则下列结论:①
.则下列结论:①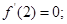 ②
②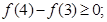 ③
③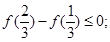 ④
④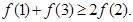 其中成立的个数是( )
其中成立的个数是( )
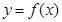 满足:当
满足:当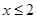 时,
时,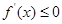 ;当
;当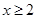 时,
时,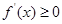 .则下列结论:①
.则下列结论:①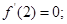 ②
②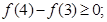 ③
③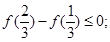 ④
④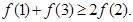 其中成立的个数是( )
其中成立的个数是( )| A.1 | B.2 | C.3 | D.4 |
D
解:根据已知条件,可知,当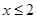 时,
时,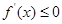 ;当
;当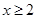 时,
时,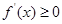 .,说明函数f(x)先减后增,并且在x=2处取得极值,因此1正确,2中利用单调性也成立,3中,利用单调性判定即满足题意,4中
.,说明函数f(x)先减后增,并且在x=2处取得极值,因此1正确,2中利用单调性也成立,3中,利用单调性判定即满足题意,4中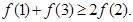 也满足单调性性质。
也满足单调性性质。
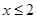 时,
时,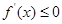 ;当
;当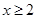 时,
时,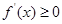 .,说明函数f(x)先减后增,并且在x=2处取得极值,因此1正确,2中利用单调性也成立,3中,利用单调性判定即满足题意,4中
.,说明函数f(x)先减后增,并且在x=2处取得极值,因此1正确,2中利用单调性也成立,3中,利用单调性判定即满足题意,4中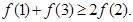 也满足单调性性质。
也满足单调性性质。
练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
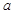 为正实数,
为正实数,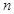 为自然数,抛物线
为自然数,抛物线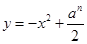 与
与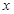 轴正半轴相交于点
轴正半轴相交于点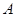 ,设
,设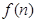 为该抛物线在点
为该抛物线在点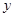 轴上的截距。
轴上的截距。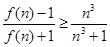 成立的
成立的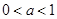 时,比较
时,比较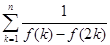 与
与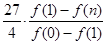 的大小,并说明理由。
的大小,并说明理由。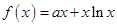 的图象在点
的图象在点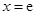 (
(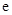 为自然对数的底数)处的切线斜率为3.
为自然对数的底数)处的切线斜率为3.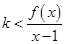 (Ⅰ)求实数
(Ⅰ)求实数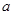 的值;
的值;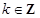 ,且 对任意
,且 对任意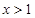 恒成立,求
恒成立,求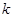 的最大值;
的最大值;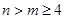 时,证明
时,证明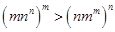 .
.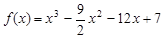 的单调递增区间.
的单调递增区间.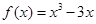 ,(1)求函数
,(1)求函数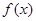 极值.(2)求函数
极值.(2)求函数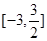 上的最大值和最小值.
上的最大值和最小值.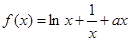 (
(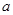 为实数).
为实数).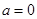 时, 求
时, 求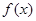 的最小值;
的最小值;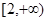 上是单调函数,求
上是单调函数,求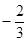 与x=1时都取得极值.
与x=1时都取得极值.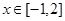 ,不等式f(x)<c2恒成立,求c的取值范围.
,不等式f(x)<c2恒成立,求c的取值范围.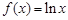 ,
,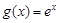 .
.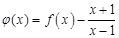 ,求函数
,求函数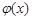 的单调区间;
的单调区间; 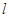 为函数
为函数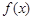 的图象上一点
的图象上一点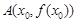 处的切线.证明:在区间
处的切线.证明:在区间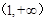 上存在唯一的
上存在唯一的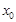 ,使得直线
,使得直线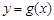 相切.
相切.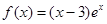 的单调递增区间是 ( )
的单调递增区间是 ( )