题目内容
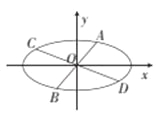
【题目】椭圆![]() 的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条线段,称为该直径的共轭直径,已知椭圆的方程为
的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条线段,称为该直径的共轭直径,已知椭圆的方程为![]() .
.
(1)若一条直径的斜率为![]() ,求该直径的共轭直径所在的直线方程;
,求该直径的共轭直径所在的直线方程;
(2)若椭圆的两条共轭直径为![]() 和
和![]() ,它们的斜率分别为
,它们的斜率分别为![]() ,证明:四边形
,证明:四边形![]() 的面积为定值.
的面积为定值.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)利用点差法计算. 设斜率为![]() 的与直径平行的弦的端点坐标分别为
的与直径平行的弦的端点坐标分别为![]() ,
,![]() ,
,
该弦中点为![]() ,将坐标代入椭圆方程,作差,然后化简得
,将坐标代入椭圆方程,作差,然后化简得![]() ,即直径的共轭直径所在的直线方程为
,即直径的共轭直径所在的直线方程为![]() ;(2)四边形
;(2)四边形![]() 显然为平行四边形,联立直线的方程和椭圆的方程,分别求得四点的坐标分别为
显然为平行四边形,联立直线的方程和椭圆的方程,分别求得四点的坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() ,然后利用两点间距离公式和点到直线距离公式,求得面积为
,然后利用两点间距离公式和点到直线距离公式,求得面积为![]() .
.
试题解析:
(1)设斜率为![]() 的与直径平行的弦的端点坐标分别为
的与直径平行的弦的端点坐标分别为![]() ,
,![]() ,
,
该弦中点为![]() ,则有
,则有![]() ,
,![]() ,
,
相减得:![]() ,
,
由于![]() ,
,![]() ,且
,且![]() ,所以得:
,所以得:![]() ,
,
故该直径的共轭直径所在的直线方程为![]() .
.
(2)椭圆的两条共轭直径为![]() 和
和![]() ,它们的斜率分别为
,它们的斜率分别为![]() ,
,
四边形![]() 显然为平行四边形,设与
显然为平行四边形,设与![]() 平行的弦的端点坐标分别为
平行的弦的端点坐标分别为![]() ,
,![]() ,
,
则![]() ,
,![]() ,而
,而![]() ,
,![]() ,
,
![]() ,故
,故![]() ,
,
由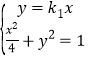 得
得![]() 的坐标分别为
的坐标分别为![]() ,
,![]()
故![]() ,同理
,同理![]() 的坐标分别为
的坐标分别为![]() ,
,![]()
设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,
,
所以,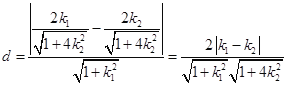 ,
,
则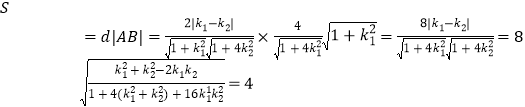 ,为定值.
,为定值.

【题目】已知圆![]() 的圆心在直线
的圆心在直线![]() 上,且圆
上,且圆![]() 经过点
经过点![]() 与点
与点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作圆
作圆![]() 的切线,求切线所在的直线的方程.
的切线,求切线所在的直线的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)求出线段![]() 的中点
的中点![]() ,进而得到线段
,进而得到线段![]() 的垂直平分线为
的垂直平分线为![]() ,与
,与![]() 联立得交点
联立得交点![]() ,∴
,∴![]() .则圆
.则圆![]() 的方程可求
的方程可求
(2)当切线斜率不存在时,可知切线方程为![]() .
.
当切线斜率存在时,设切线方程为![]() ,由
,由![]() 到此直线的距离为
到此直线的距离为![]() ,解得
,解得![]() ,即可到切线所在直线的方程.
,即可到切线所在直线的方程.
试题解析:((1)设 线段![]() 的中点为
的中点为![]() ,∵
,∵![]() ,
,
∴线段![]() 的垂直平分线为
的垂直平分线为![]() ,与
,与![]() 联立得交点
联立得交点![]() ,
,
∴![]() .
.
∴圆![]() 的方程为
的方程为![]() .
.
(2)当切线斜率不存在时,切线方程为![]() .
.
当切线斜率存在时,设切线方程为![]() ,即
,即![]() ,
,
则![]() 到此直线的距离为
到此直线的距离为![]() ,解得
,解得![]() ,∴切线方程为
,∴切线方程为![]() .
.
故满足条件的切线方程为![]() 或
或![]() .
.
【点睛】本题考查圆的方程的求法,圆的切线,中点弦等问题,解题的关键是利用圆的特性,利用点到直线的距离公式求解.
【题型】解答题
【结束】
20
【题目】某小型企业甲产品生产的投入成本![]() (单位:万元)与产品销售收入
(单位:万元)与产品销售收入![]() (单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
(单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
| 7 | 10 | 11 | 15 | 17 |
| 19 | 22 | 25 | 30 | 34 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本20万元的毛利率更大还是投入成本24万元的毛利率更大(![]() )?
)?
相关公式: 
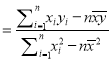 ,
, ![]() .
.