题目内容
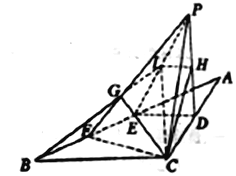
【题目】如图,在三棱锥![]() 中,
中, ![]() 两两垂直且相等,过
两两垂直且相等,过![]() 的中点
的中点![]() 作平面
作平面![]() ∥
∥![]() ,且
,且![]() 分别交PB,PC于M、N,交
分别交PB,PC于M、N,交![]() 的延长线于
的延长线于![]() .
.
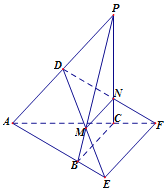
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)运用线面垂直的判定和性质定理,以及线面平行的性质定理,即可得证;
(Ⅱ)以CA,CB,CP分别为x,y,z轴建立空间直角坐标系,并设BC=2,求出点A,B,P,D,E,F的坐标,设平面PAB的法向量和平面DEF的法向量,由向量垂直的条件:数量积为0,即可得到法向量,再由向量的夹角公式,即可得到所求二面角的余弦值.
解析:
(1)证明:由BC⊥PC,BC⊥AC可知:BC⊥平面PAC,
又因为平面α∥BC,平面AEF过BC且与平面α交于EF,
所以EF∥BC.故EF⊥平面PAC;
(2)以CA,CB,CP分别为x,y,z轴建立空间直角坐标系,
并设BC=2.则A(2,0,0),B(0,2,0),P(0,0,2),
设平面PAB的法向量![]() ,
, ![]()
D(1,0,1),E(﹣1,3,0),F(﹣1,0,0),
设平面DEF的法向量![]() ,
,
![]()
![]()
二面角P﹣DM﹣N的余弦值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目