题目内容
【题目】设椭圆C: ![]() =1的离心率e=
=1的离心率e= ![]() ,动点P在椭圆C上,点P到椭圆C的两个焦点的距离之和是4.
,动点P在椭圆C上,点P到椭圆C的两个焦点的距离之和是4.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若椭圆C1的方程为 ![]() =1(m>n>0),椭圆C2的方程为
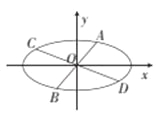
=1(m>n>0),椭圆C2的方程为 ![]() =λ(λ>0,且λ≠1),则称椭圆C2是椭圆C1的λ倍相似椭圆.已知椭圆C2是椭圆C的3倍相似椭圆.若过椭圆C上动点P的切线l交椭圆C2于A,B两点,O为坐标原点,试证明当切线l变化时|PA|=|PB|并研究△OAB面积的变化情况.
=λ(λ>0,且λ≠1),则称椭圆C2是椭圆C1的λ倍相似椭圆.已知椭圆C2是椭圆C的3倍相似椭圆.若过椭圆C上动点P的切线l交椭圆C2于A,B两点,O为坐标原点,试证明当切线l变化时|PA|=|PB|并研究△OAB面积的变化情况.
【答案】解:(Ⅰ)依题意,e= ![]() =
= ![]() ,
,
由椭圆的定义可得2a=4,即a=2,
即有c=1,b2=a2﹣c2=3,
则椭圆C方程为: ![]() =1;
=1;
(Ⅱ)椭圆C的3倍相似椭圆C2的方程为: ![]() =3;
=3;
①若切线l垂直于x轴,则其方程为:x=±2,解得y=± ![]() ,
,
显然|PA|=|PB|,|AB|=2 ![]() ,△OAB面积为
,△OAB面积为 ![]() ×2×2
×2×2 ![]() =2
=2 ![]() ;
;
②若切线l不垂直于x轴,可设其方程为:y=kx+m.
将y=kx+m代人椭圆C方程,得:(3+4k2)x2+8kmx+4m2﹣12=0,
△=(8km)2﹣4(3+4k2)(4m2﹣12)=48(4k2+3﹣m2)=0,
即m2=4k2+3,
设A,B两点的坐标分别是(x1 , y1),(x2 , y2),
将y=kx+m代入椭圆C2的方程,得:(3+4k2)x2+8kmx+4m2﹣36=0,
此时x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
则AB的中点为(﹣ ![]() ,
, ![]() ),即为(﹣
),即为(﹣ ![]() ,
, ![]() ),
),
代入椭圆C的方程,可得 ![]() +
+ ![]() =
= ![]() =
= ![]() =1,
=1,
满足椭圆方程,则|PA|=|PB|成立;
即有|AB|= ![]() |x1﹣x2|=
|x1﹣x2|= ![]()
![]()
= ![]()
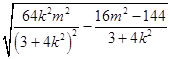
= ![]()
![]() =
= ![]()
![]() .
.
又点O到直线l的距离d= ![]() ,
,
可得S△OAB= ![]() |AB|d=2
|AB|d=2 ![]() ,
,
综上,当切线l变化时,△OAB的面积为定值2 ![]()
【解析】(Ⅰ)由椭圆的定义可得a=2,再由离心率公式和a,b,c的关系,即可得到b,进而得到椭圆方程;(Ⅱ)依题意,求得椭圆C2方程,讨论直线的斜率不存在,得到|PA|=|PB|和面积为定值;当切线l的斜率存在时,设l的方程为:y=kx+m,代入椭圆C2方程,运用韦达定理和中点坐标公式,可得|PA|=|PB|,由弦长公式,和点到直线的距离公式,结合面积公式,计算即可得到面积为定值.

【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算电费每月用电不超过100度仍按原标准收费,超过的部分每度按0.5元计算.
Ⅰ.设月用电x度时,应交电费y元,写出y关于x的函数关系式;
Ⅱ.小明家第一季度缴纳电费情况如下:
月份 | 一月 | 二月 | 三月 | 合计 |
缴费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
问小明家第一季度共用多少度?