题目内容
已知函数f(x)=x|m-x|(x∈R),且f(4)=0.
(1)求实数m的值;
(2)作出函数f(x)的图象并判断其零点个数;
(3)根据图象指出f(x)的单调递减区间;
(4)根据图象写出不等式f(x)>0的解集;
(5)求集合M={m|使方程f(x)=m有三个不相等的实根}.
(1)求实数m的值;
(2)作出函数f(x)的图象并判断其零点个数;
(3)根据图象指出f(x)的单调递减区间;
(4)根据图象写出不等式f(x)>0的解集;
(5)求集合M={m|使方程f(x)=m有三个不相等的实根}.

(1)m=4
(2)两个零点
(3)[2,4]
(4){x|0<x<4或x>4}
(5)M={m|0<m<4}
(2)两个零点
(3)[2,4]
(4){x|0<x<4或x>4}
(5)M={m|0<m<4}
解:(1)∵f(4)=0,∴4|m-4|=0,即m=4.
(2)∵f(x)=x|m-x|=x|4-x|=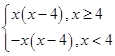
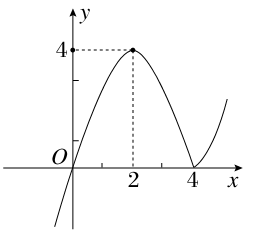
∴函数f(x)的图象如图.
由图象知f(x)有两个零点.
(3)f(x)的单调递减区间为[2,4].
(4)f(x)>0的解集为:{x|0<x<4或x>4}.
(5)M={m|0<m<4}.
(2)∵f(x)=x|m-x|=x|4-x|=
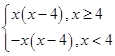
∴函数f(x)的图象如图.
由图象知f(x)有两个零点.
(3)f(x)的单调递减区间为[2,4].
(4)f(x)>0的解集为:{x|0<x<4或x>4}.
(5)M={m|0<m<4}.

练习册系列答案
相关题目
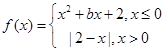 ,
,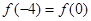 ,则函数
,则函数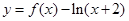 的零点有
的零点有 个.
个.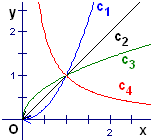
 ,其中
,其中 ,
, 为自然对数的底数.
为自然对数的底数. 是函数
是函数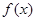 的导函数,求函数
的导函数,求函数 上的最小值;
上的最小值; ,函数
,函数 内有零点,求
内有零点,求 的取值范围
的取值范围 -
- (a>0)没有零点,则实数a的取值范围为________.
(a>0)没有零点,则实数a的取值范围为________. )x-sinx在区间[0,2π]上的零点个数为( )
)x-sinx在区间[0,2π]上的零点个数为( ) x=
x= 的解x0∈
的解x0∈ ,则正整数n=________.
,则正整数n=________.