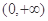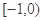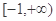题目内容

若函数f(x)=|4x-x2|-a的零点个数为4，则a的取值范围是（   ）
A．[0,3]B．(0，4）C．[-1,2]D．(-1,4)
B
函数f(x)=|4x-x2|-a的零点个数为4方程|4x-x2|-a=0有4个不同的根a=|4x-x2|函数g(x)=a与函数F(x)=|4x-x2|的图象有4个不同的交点

作出4x-x2的图象,可知在x=2处其有最大值4
∴若直线g(x)=a与函数F(x)=|4x-x2|的图象有4个不同的交点,则a∈(0,4)
练习册系列答案
相关题目
已知函数f(x)＝x|m－x|(x∈R)，且f(4)＝0.
(1)求实数m的值；
(2)作出函数f(x)的图象并判断其零点个数；
(3)根据图象指出f(x)的单调递减区间；
(4)根据图象写出不等式f(x)>0的解集；
(5)求集合M＝{m|使方程f(x)＝m有三个不相等的实根}．
（13分）（2011•湖北）设函数f（x）=x3+2ax2+bx+a，g（x）=x2﹣3x+2，其中x∈R，a、b为常数，已知曲线y=f（x）与y=g（x）在点（2，0）处有相同的切线l．
（Ⅰ） 求a、b的值，并写出切线l的方程；
（Ⅱ）若方程f（x）+g（x）=mx有三个互不相同的实根0、x1、x2，其中x1＜x2，且对任意的x∈[x1，x2]，f（x）+g（x）＜m（x﹣1）恒成立，求实数m的取值范围．
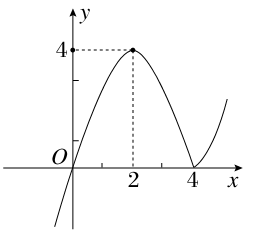
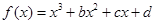如图是函数的大致图象，则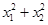等于
A．B．C．D．
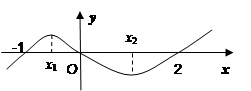
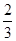
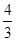
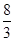
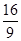
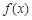已知奇函数是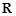上的单调函数，若函数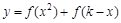只有一个零点，则实数k的值是
     ．
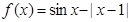函数的零点个数为       ．
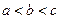若，则函数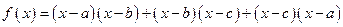的两个零点分别位于区间(  )
A．(a，b)和(b，c)内
B．(－∞，a)和(a，b)内
C．(b，c)和(c，+∞)内
D．(－∞，a)和(c，+∞)内
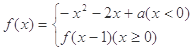已知函数,且函数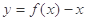恰有3个不同的零点,则实数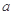的取值范围是（     ）
A．B．C．D．
函数f(x)＝x2＋4x＋a没有零点，则实数a的取值范围是(　　)
A．a<4B．a>4C．a≤4 D．a≥4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网