题目内容
已知函数 ,其中
,其中 ,
, 为自然对数的底数.
为自然对数的底数.
(Ⅰ)设 是函数
是函数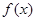 的导函数,求函数
的导函数,求函数 在区间
在区间 上的最小值;
上的最小值;
(Ⅱ)若 ,函数
,函数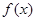 在区间
在区间 内有零点,求
内有零点,求 的取值范围
的取值范围
 ,其中
,其中 ,
, 为自然对数的底数.
为自然对数的底数.(Ⅰ)设
 是函数
是函数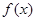 的导函数,求函数
的导函数,求函数 在区间
在区间 上的最小值;
上的最小值;(Ⅱ)若
 ,函数
,函数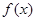 在区间
在区间 内有零点,求
内有零点,求 的取值范围
的取值范围(Ⅰ)当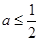 时,
时,  ;当
;当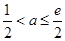 时,
时, 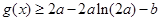 ;
;
当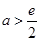 时,
时, 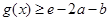 .(Ⅱ)
.(Ⅱ) 的范围为
的范围为 .
.
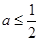 时,
时,  ;当
;当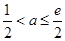 时,
时, 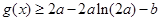 ;
;当
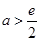 时,
时, 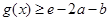 .(Ⅱ)
.(Ⅱ) 的范围为
的范围为 .
.试题分析:(Ⅰ)易得
 ,再对分
,再对分 情况确定
情况确定 的单调区间,根据
的单调区间,根据 在
在 上的单调性即可得
上的单调性即可得 在
在 上的最小值.(Ⅱ)设
上的最小值.(Ⅱ)设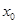 为
为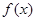 在区间
在区间 内的一个零点,注意到
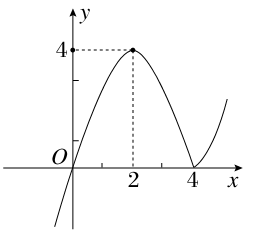
内的一个零点,注意到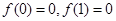 .联系到函数的图象可知,导函数
.联系到函数的图象可知,导函数 在区间
在区间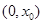 内存在零点
内存在零点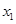 ,
, 在区间
在区间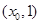 内存在零点
内存在零点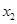 ,即
,即 在区间
在区间 内至少有两个零点. 由(Ⅰ)可知,当
内至少有两个零点. 由(Ⅰ)可知,当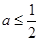 及
及 时,
时, 在
在 内都不可能有两个零点.所以
内都不可能有两个零点.所以 .此时,
.此时, 在
在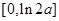 上单调递减,在
上单调递减,在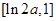 上单调递增,因此
上单调递增,因此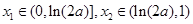 ,且必有
,且必有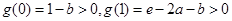 .由
.由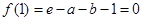 得:
得: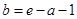 ,代入这两个不等式即可得
,代入这两个不等式即可得 的取值范围.
的取值范围.试题解答:(Ⅰ)

①当
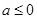 时,
时,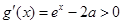 ,所以
,所以 .
.②当
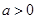 时,由
时,由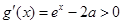 得
得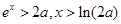 .
.若
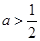 ,则
,则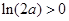 ;若
;若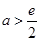 ,则
,则 .
.所以当
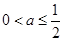 时,
时, 在
在 上单调递增,所以
上单调递增,所以 .
.当
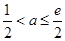 时,
时, 在
在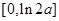 上单调递减,在
上单调递减,在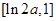 上单调递增,所以
上单调递增,所以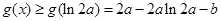 .
.当
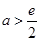 时,
时, 在
在 上单调递减,所以
上单调递减,所以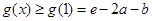 .
.(Ⅱ)设
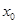 为
为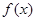 在区间
在区间 内的一个零点,则由
内的一个零点,则由 可知,
可知,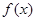 在区间
在区间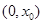 上不可能单调递增,也不可能单调递减.
上不可能单调递增,也不可能单调递减.则
 不可能恒为正,也不可能恒为负.
不可能恒为正,也不可能恒为负.故
 在区间
在区间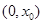 内存在零点
内存在零点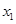 .
.同理
 在区间
在区间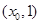 内存在零点
内存在零点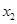 .
.所以
 在区间
在区间 内至少有两个零点.
内至少有两个零点. 由(Ⅰ)知,当
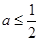 时,
时, 在
在 上单调递增,故
上单调递增,故 在
在 内至多有一个零点.
内至多有一个零点.当
 时,
时, 在
在 上单调递减,故
上单调递减,故 在
在 内至多有一个零点.
内至多有一个零点.所以
 .
.此时,
 在
在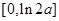 上单调递减,在
上单调递减,在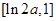 上单调递增,
上单调递增,因此
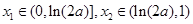 ,必有
,必有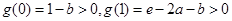 .
.由
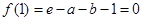 得:
得: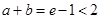 ,有
,有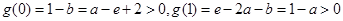 .
.解得
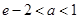 .
.当
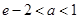 时,
时, 在区间
在区间 内有最小值
内有最小值 .
.若
 ,则
,则 ,
,从而
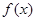 在区间
在区间 上单调递增,这与
上单调递增,这与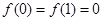 矛盾,所以
矛盾,所以 .
.又
 ,
,故此时
 在
在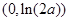 和
和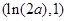 内各只有一个零点
内各只有一个零点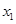 和
和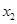 .
.由此可知
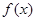 在
在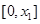 上单调递增,在
上单调递增,在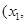
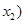 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.所以
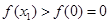 ,
,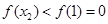 ,
,故
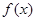 在
在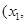
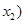 内有零点.
内有零点.综上可知,
 的取值范围是
的取值范围是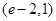 .
.【考点定位】导数的应用及函数的零点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 的简图;
的简图; 有三个不等实根,求k值的集合;
有三个不等实根,求k值的集合; 时,函数
时,函数 的下方,试求出k值的集合。
的下方,试求出k值的集合。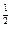 的图象经过的“卦限”是 .
的图象经过的“卦限”是 . 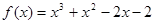 的一个正数零点附近的函数值的参考数据如下:
的一个正数零点附近的函数值的参考数据如下: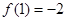
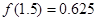
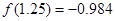
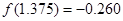
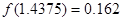
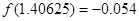
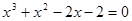 的一个近似根(精确到0.1)为( )
的一个近似根(精确到0.1)为( ) 关于
关于 的方程
的方程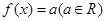 的解的个数不可能是( )
的解的个数不可能是( ) 若函数
若函数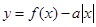 恰有4个零点,则实数
恰有4个零点,则实数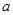 的取值范围为_______
的取值范围为_______ 若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )
若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )