题目内容
已知抛物线的顶点在原点,焦点在y轴的负半轴上,过其上一点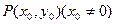 的切线方程为
的切线方程为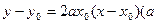 为常数).
为常数).
(I)求抛物线方程;
(II)斜率为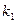 的直线PA与抛物线的另一交点为A,斜率为
的直线PA与抛物线的另一交点为A,斜率为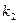 的直线PB与抛物线的另一交点为B(A、B两点不同),且满足
的直线PB与抛物线的另一交点为B(A、B两点不同),且满足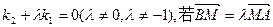 ,求证线段PM的中点在y轴上;
,求证线段PM的中点在y轴上;
(III)在(II)的条件下,当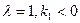 时,若P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标的取值范围.
时,若P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标的取值范围.
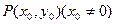 的切线方程为
的切线方程为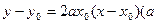 为常数).
为常数).(I)求抛物线方程;
(II)斜率为
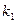 的直线PA与抛物线的另一交点为A,斜率为
的直线PA与抛物线的另一交点为A,斜率为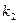 的直线PB与抛物线的另一交点为B(A、B两点不同),且满足
的直线PB与抛物线的另一交点为B(A、B两点不同),且满足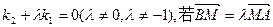 ,求证线段PM的中点在y轴上;
,求证线段PM的中点在y轴上;(III)在(II)的条件下,当
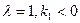 时,若P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标的取值范围.
时,若P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标的取值范围. (1) (2)线段PM的中点在y轴上(3)
(2)线段PM的中点在y轴上(3)
 (2)线段PM的中点在y轴上(3)
(2)线段PM的中点在y轴上(3)
(I)由题意可设抛物线的方程为 ,
,
∵过点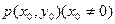 的切线方程为
的切线方程为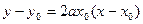 ,
,
 ……………………………………………………………2分
……………………………………………………………2分

∴抛物线的方程为 …………………………………………………3分
…………………………………………………3分
(II)直线PA的方程为 ,
,
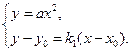

同理,可得 . …………………………………………………………5分
. …………………………………………………………5分
 …………………………6分
…………………………6分
又

∴线段PM的中点在y轴上.………………………………………………………7分
(III)由

 ………………………………………8分
………………………………………8分
∵∠PAB为钝角,且P, A, B不共线,

即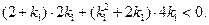
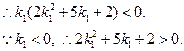
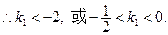 …………………………………………………………10分
…………………………………………………………10分
又∵点A的纵坐标 ∴当
∴当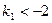 时,
时, ;
;
当
∴∠PAB为钝角时点A的坐标的取值范围为 ……………12分
……………12分
 ,
,∵过点
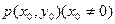 的切线方程为
的切线方程为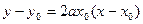 ,
, ……………………………………………………………2分
……………………………………………………………2分
∴抛物线的方程为
 …………………………………………………3分
…………………………………………………3分(II)直线PA的方程为
 ,
,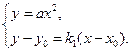

同理,可得
 . …………………………………………………………5分
. …………………………………………………………5分 …………………………6分
…………………………6分又


∴线段PM的中点在y轴上.………………………………………………………7分
(III)由


 ………………………………………8分
………………………………………8分∵∠PAB为钝角,且P, A, B不共线,

即
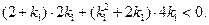
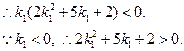
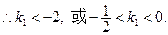 …………………………………………………………10分
…………………………………………………………10分又∵点A的纵坐标
 ∴当
∴当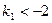 时,
时, ;
;当

∴∠PAB为钝角时点A的坐标的取值范围为
 ……………12分
……………12分
练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
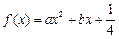 与直线
与直线 相切于点
相切于点 .
.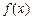 的解析式;
的解析式; ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.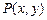 到点
到点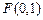 与到直线
与到直线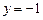 的距离相等,求点
的距离相等,求点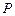 的轨迹
的轨迹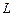 的方程;
的方程;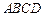 的三个顶点
的三个顶点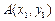 ,
,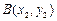 ,
,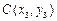 (
(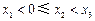 )在(1)中的曲线
)在(1)中的曲线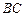 的斜率为
的斜率为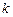 ,
,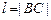 ,求
,求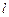 关于
关于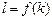 ;
;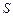 的最小值.
的最小值.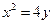 上一点
上一点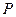 到焦点的距离为2,则点
到焦点的距离为2,则点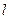 过抛物线的焦点F,交抛物线与A、B两点, 且
过抛物线的焦点F,交抛物线与A、B两点, 且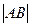 ="4p" ,求直线
="4p" ,求直线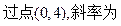 -1的直线与抛物线
-1的直线与抛物线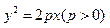 交于两点A,B,如果
交于两点A,B,如果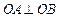 (O为原点)求P的值及抛物线的焦点坐标。
(O为原点)求P的值及抛物线的焦点坐标。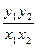 的值为________________.
的值为________________.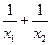
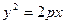 上,横坐标为2的点到抛物线焦点的距离为3,则
上,横坐标为2的点到抛物线焦点的距离为3,则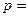 。
。