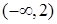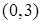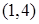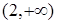题目内容
已知函数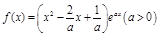
(Ⅰ)当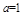 时,求函数
时,求函数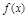 的图象在点
的图象在点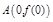 处的切线方程;
处的切线方程;
(Ⅱ)讨论函数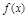 的单调性;
的单调性;
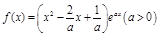
(Ⅰ)当
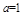 时,求函数
时,求函数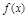 的图象在点
的图象在点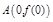 处的切线方程;
处的切线方程;(Ⅱ)讨论函数
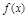 的单调性;
的单调性;(Ⅰ)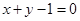 (Ⅱ)
(Ⅱ)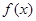 在
在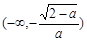 ,
,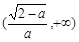 为增函数,
为增函数,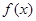 在
在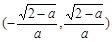 为减函数
为减函数
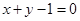 (Ⅱ)
(Ⅱ)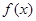 在
在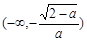 ,
,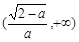 为增函数,
为增函数,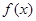 在
在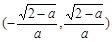 为减函数
为减函数本试题主要是考查了导数在研究函数中的运用。
(1)利用导数的几何意义表示切线方程关键是切点和切点出的斜率值。
(2)求解导数,然后对于含有参数的二次不等式的解集进行分类讨论得到。
解:(I)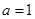 时,
时, ,
,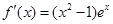
于是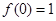 ,
,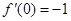 ,
,
所以函数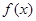 的图象在点
的图象在点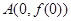 处的切线方程为
处的切线方程为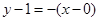 ,即
,即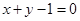 .
.
(II)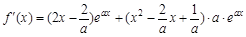
=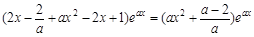 ,
,
∵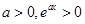 ,∴ 只需讨论
,∴ 只需讨论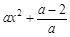 的符号.
的符号.
ⅰ)当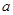 >2时,
>2时,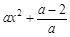 >0,这时
>0,这时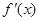 >0,所以函数
>0,所以函数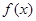 在(-∞,+∞)上为增函数.ⅱ)当
在(-∞,+∞)上为增函数.ⅱ)当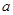 = 2时,
= 2时,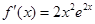 ≥0,函数
≥0,函数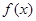 在(-∞,+∞)上为增函数.
在(-∞,+∞)上为增函数.
ⅲ)当0<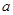 <2时,令
<2时,令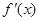 = 0,解得
= 0,解得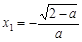 ,
,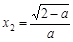 .
.
当 变化时,
变化时,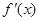 和
和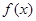 的变化情况如下表:
的变化情况如下表:
∴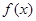 在
在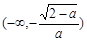 ,
,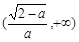 为增函数,
为增函数,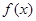 在
在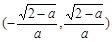 为减函数;
为减函数;
【备注题】(Ⅲ)是否存在实数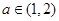 ,使
,使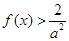 当
当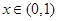 时恒成立?若存在,求出实数
时恒成立?若存在,求出实数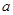 ;若不存在,请说明理由.
;若不存在,请说明理由.
当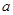 ∈(1,2)时,
∈(1,2)时,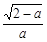 ∈(0,1).由(2)知
∈(0,1).由(2)知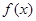 在
在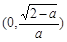 上是减函数,在
上是减函数,在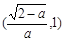 上是增函数,故当
上是增函数,故当 ∈(0,1)时,
∈(0,1)时,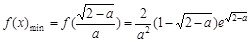 ,所以
,所以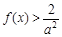 当
当 ∈(0,1)时恒成立,等价于
∈(0,1)时恒成立,等价于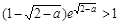 恒成立.
恒成立.
当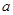 ∈(1,2)时,
∈(1,2)时,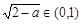 ,设
,设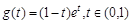 ,则
,则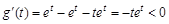 ,表明g(t) 在(0,1)上单调递减,于是可得
,表明g(t) 在(0,1)上单调递减,于是可得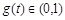 ,即
,即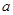 ∈(1,2)时
∈(1,2)时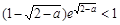 恒成立,因此,符合条件的实数
恒成立,因此,符合条件的实数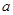 不存在.
不存在.
(1)利用导数的几何意义表示切线方程关键是切点和切点出的斜率值。
(2)求解导数,然后对于含有参数的二次不等式的解集进行分类讨论得到。
解:(I)
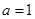 时,
时, ,
,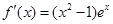
于是
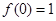 ,
,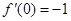 ,
,所以函数
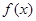 的图象在点
的图象在点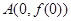 处的切线方程为
处的切线方程为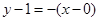 ,即
,即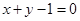 .
. (II)
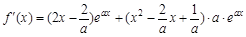
=
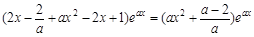 ,
,∵
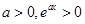 ,∴ 只需讨论
,∴ 只需讨论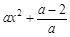 的符号.
的符号. ⅰ)当
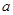 >2时,
>2时,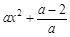 >0,这时
>0,这时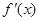 >0,所以函数
>0,所以函数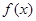 在(-∞,+∞)上为增函数.ⅱ)当
在(-∞,+∞)上为增函数.ⅱ)当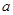 = 2时,
= 2时,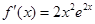 ≥0,函数
≥0,函数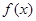 在(-∞,+∞)上为增函数.
在(-∞,+∞)上为增函数.ⅲ)当0<
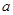 <2时,令
<2时,令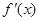 = 0,解得
= 0,解得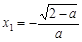 ,
,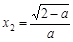 .
.当
 变化时,
变化时,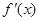 和
和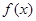 的变化情况如下表:
的变化情况如下表: | 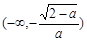 | 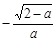 | 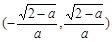 | 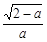 | 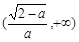 |
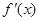 | + | 0 | - | 0 | + |
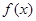 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
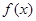 在
在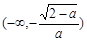 ,
,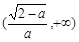 为增函数,
为增函数,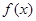 在
在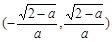 为减函数;
为减函数;【备注题】(Ⅲ)是否存在实数
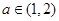 ,使
,使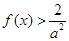 当
当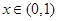 时恒成立?若存在,求出实数
时恒成立?若存在,求出实数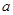 ;若不存在,请说明理由.
;若不存在,请说明理由.当
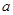 ∈(1,2)时,
∈(1,2)时,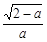 ∈(0,1).由(2)知
∈(0,1).由(2)知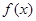 在
在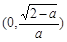 上是减函数,在
上是减函数,在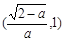 上是增函数,故当
上是增函数,故当 ∈(0,1)时,
∈(0,1)时,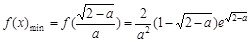 ,所以
,所以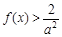 当
当 ∈(0,1)时恒成立,等价于
∈(0,1)时恒成立,等价于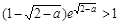 恒成立.
恒成立. 当
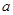 ∈(1,2)时,
∈(1,2)时,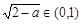 ,设
,设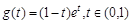 ,则
,则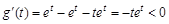 ,表明g(t) 在(0,1)上单调递减,于是可得
,表明g(t) 在(0,1)上单调递减,于是可得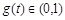 ,即
,即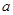 ∈(1,2)时
∈(1,2)时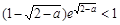 恒成立,因此,符合条件的实数
恒成立,因此,符合条件的实数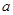 不存在.
不存在. 
练习册系列答案
相关题目
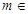 R,函数
R,函数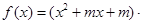 e
e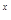 .
. 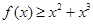 .
.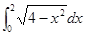 的结果是( )
的结果是( )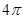
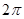
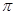
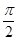

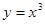 在点P处的切线的斜率等于3,则点P的坐标为( )
在点P处的切线的斜率等于3,则点P的坐标为( )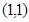 或
或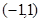
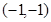 或
或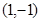
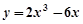 的极大值等于 .
的极大值等于 .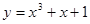 在点(1,3)处的切线方程是( )
在点(1,3)处的切线方程是( )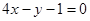
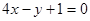
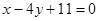
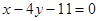
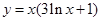 在点
在点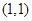 处的切线方程为__________________ .
处的切线方程为__________________ .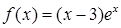 的单调增区间是
的单调增区间是