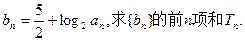题目内容
(本题满分13分) 设函数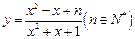 的最小值为
的最小值为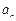 ,最大值为
,最大值为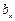 ,又
,又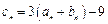
(1)求数列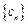 的通项公式;
的通项公式;
(2)设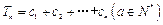 ,求
,求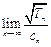 的值;
的值;
(3)设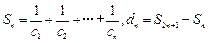 ,是否存在最小的整数
,是否存在最小的整数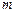 ,使对
,使对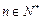 ,有
,有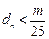 成立?若存在,求出
成立?若存在,求出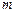 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
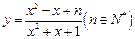 的最小值为
的最小值为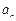 ,最大值为
,最大值为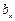 ,又
,又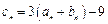
(1)求数列
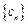 的通项公式;
的通项公式;(2)设
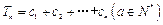 ,求
,求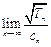 的值;
的值;(3)设
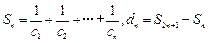 ,是否存在最小的整数
,是否存在最小的整数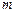 ,使对
,使对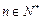 ,有
,有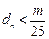 成立?若存在,求出
成立?若存在,求出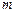 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。(1)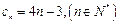 (2)
(2) (3)8
(3)8
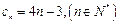 (2)
(2) (3)8
(3)8(1)函数 可变形为
可变形为 ①
①
当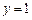 时,方程有解;当
时,方程有解;当 时,方程①有解,由
时,方程①有解,由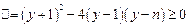
得,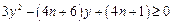 且
且 ②由题意不等式②的解集为
②由题意不等式②的解集为 ,即
,即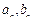 为方程
为方程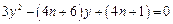 的两根,则
的两根,则 于是
于是 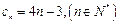
(2)由(1)可得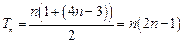
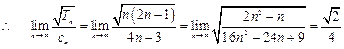
(3)因为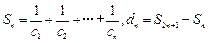
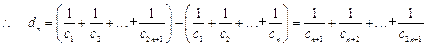


所以,数列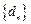 为递减数列从而数列
为递减数列从而数列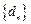 的最大项为
的最大项为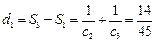 要使对
要使对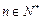 恒成立,只要
恒成立,只要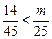 ,得
,得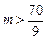 因此对
因此对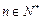 ,有
,有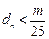 成立的最小的整数
成立的最小的整数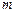 为8.
为8.
 可变形为
可变形为 ①
①当
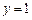 时,方程有解;当
时,方程有解;当 时,方程①有解,由
时,方程①有解,由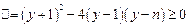
得,
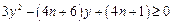 且
且 ②由题意不等式②的解集为
②由题意不等式②的解集为 ,即
,即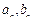 为方程
为方程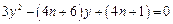 的两根,则
的两根,则 于是
于是 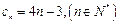
(2)由(1)可得
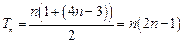
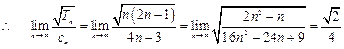
(3)因为
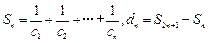
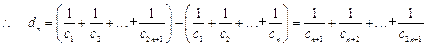


所以,数列
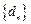 为递减数列从而数列
为递减数列从而数列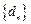 的最大项为
的最大项为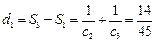 要使对
要使对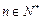 恒成立,只要
恒成立,只要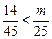 ,得
,得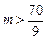 因此对
因此对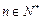 ,有
,有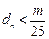 成立的最小的整数
成立的最小的整数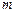 为8.
为8.
练习册系列答案
相关题目
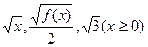 成等差数列.又数列
成等差数列.又数列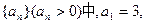 此数列的前n项的和Sn(
此数列的前n项的和Sn(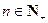 )对所有大于1的正整数n都有
)对所有大于1的正整数n都有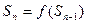 .(1)求数列
.(1)求数列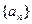 的第n+1项;(2)若
的第n+1项;(2)若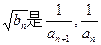 的等比中项,且Tn为{bn}的前n项和,求Tn.
的等比中项,且Tn为{bn}的前n项和,求Tn. ,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4 (Ⅰ)求证:数列{bn}中的每一项都是数列{an}中的项;
,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4 (Ⅰ)求证:数列{bn}中的每一项都是数列{an}中的项; ,求数列{cn}的前n项的和Tn
,求数列{cn}的前n项的和Tn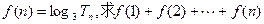 的最大值.
的最大值.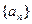 中,前n项和为
中,前n项和为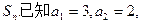
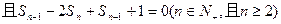
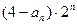 }的前n项和Tn.
}的前n项和Tn. 中,已知
中,已知 .
. 且
且 的前项
的前项 和为
和为 ,求证:
,求证: .
.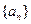 的前
的前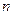 项和
项和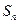 和通项
和通项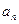 满足
满足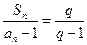 (
(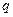 是常数且
是常数且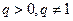 )。(Ⅰ)求数列
)。(Ⅰ)求数列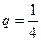 时,试证明
时,试证明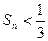 ;
;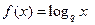 ,
,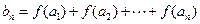 ,是否存在正整数
,是否存在正整数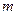 ,使
,使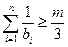 对
对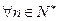 都成立?若存在,求出
都成立?若存在,求出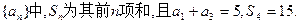 (I)求数列
(I)求数列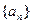 的通项公式; (II)设
的通项公式; (II)设