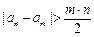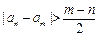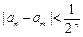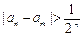题目内容
(本小题满分12分)已知等差数列{an}的首项 ,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4 (Ⅰ)求证:数列{bn}中的每一项都是数列{an}中的项;
,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4 (Ⅰ)求证:数列{bn}中的每一项都是数列{an}中的项;
(Ⅱ)若a1=2,设 ,求数列{cn}的前n项的和Tn
,求数列{cn}的前n项的和Tn
(Ⅲ)在(Ⅱ)的条件下,若有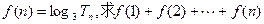 的最大值.
的最大值.
 ,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4 (Ⅰ)求证:数列{bn}中的每一项都是数列{an}中的项;
,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4 (Ⅰ)求证:数列{bn}中的每一项都是数列{an}中的项;(Ⅱ)若a1=2,设
 ,求数列{cn}的前n项的和Tn
,求数列{cn}的前n项的和Tn(Ⅲ)在(Ⅱ)的条件下,若有
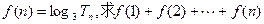 的最大值.
的最大值. (I) 略 (Ⅱ)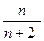 (III)最大值为-1
(III)最大值为-1
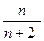 (III)最大值为-1
(III)最大值为-1(Ⅰ)设等差数列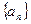 的公差为d,由
的公差为d,由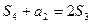 ,得
,得
 ,
, ,…………2分
,…………2分
则 ,
,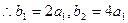 ,
,
等比数列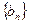 的公比
的公比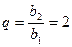 ,……3分则
,……3分则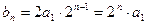 ,……4分
,……4分
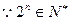 ,
,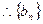 中的每一项都是
中的每一项都是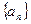 中的项……………5分
中的项……………5分
(Ⅱ)当 时,
时, ,
,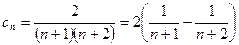 …7分
…7分
则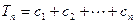 =
= =
=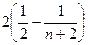 =
=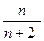 8分
8分
(Ⅲ)
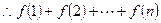
=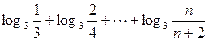 =
=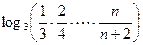 =
=
 ………10分
………10分
 。即
。即 的最大值为-1…12分
的最大值为-1…12分
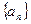 的公差为d,由
的公差为d,由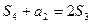 ,得
,得 ,
, ,…………2分
,…………2分则
 ,
,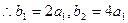 ,
,等比数列
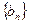 的公比
的公比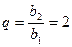 ,……3分则
,……3分则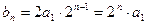 ,……4分
,……4分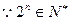 ,
,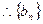 中的每一项都是
中的每一项都是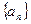 中的项……………5分
中的项……………5分(Ⅱ)当
 时,
时, ,
,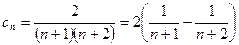 …7分
…7分则
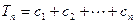 =
= =
=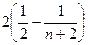 =
=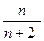 8分
8分(Ⅲ)

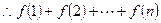
=
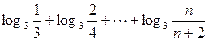 =
=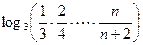 =
=
 ………10分
………10分 。即
。即 的最大值为-1…12分
的最大值为-1…12分
练习册系列答案
相关题目
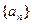 是正项等差数列,若
是正项等差数列,若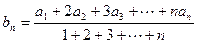 ,则数列
,则数列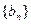 也为等差数列,类比上述结论,写出正项等比数列
也为等差数列,类比上述结论,写出正项等比数列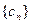 ,若
,若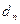 = ,则数列
= ,则数列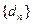 也为等比数列。
也为等比数列。
 小题满分14分)已知
小题满分14分)已知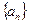 是正数组成的数列,
是正数组成的数列,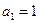 ,且点(
,且点(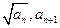 )(n
)(n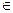 N*)在
N*)在 函数
函数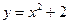 的图象上.(Ⅰ)求数列
的图象上.(Ⅰ)求数列 (Ⅱ)若
(Ⅱ)若
 数列
数列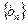
 满足
满足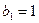 ,
,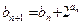 ,求数列
,求数列
 ,将
,将 的图象按
的图象按 平移后得一奇函数 (Ⅰ)求当
平移后得一奇函数 (Ⅰ)求当 时函数
时函数 的值域 (Ⅱ)设数列
的值域 (Ⅱ)设数列 的通项公式为
的通项公式为
 ,
, 为其前
为其前 项的和, 求
项的和, 求 的值
的值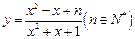 的最小值为
的最小值为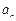 ,最大值为
,最大值为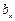 ,又
,又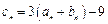
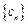 的通项公式;
的通项公式;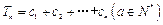 ,求
,求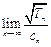 的值;
的值;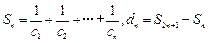 ,是否存在最小的整数
,是否存在最小的整数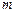 ,使对
,使对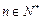 ,有
,有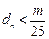 成立?若存在,求出
成立?若存在,求出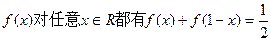 (I)求
(I)求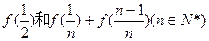 的值;(II)数列{an}满足
的值;(II)数列{an}满足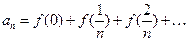
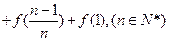 数列{an}是等差数列吗?请给予证明;
数列{an}是等差数列吗?请给予证明;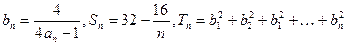 ,试比较Tn与Sn的大小.
,试比较Tn与Sn的大小.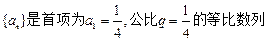 ,设
,设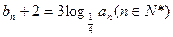 ,数列
,数列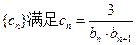 .(Ⅰ)求数列
.(Ⅰ)求数列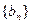 的通项公式;(Ⅱ)若数列
的通项公式;(Ⅱ)若数列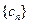 的前
的前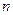 项和为
项和为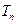 ,求
,求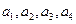 成等差数列,且
成等差数列,且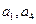 为方程方程
为方程方程 的两根,则
的两根,则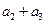 等于 。
等于 。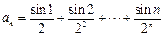 ,则对任意正整数
,则对任意正整数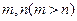 都成立的是( )
都成立的是( )