题目内容
【题目】如图,正方体ABCD﹣A1B1C1D1中,E是DD1的中点. 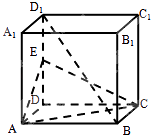
(1)求证:BD1∥平面AEC.
(2)求异面直线BC1与AC所成的角.
【答案】
(1)解:连结BD交AC于O,则O为BD的中点,
连EO,因为E是DD1的中点,所以EO∥BD1,
又EO面AEC,BD1面AEC,
所以BD1∥平面AEC
(2)解:连结AD1、CD1,
∵正方体ABCD﹣A1B1C1D1中,AB ![]() C1D1,
C1D1,
∴四边形ABC1D1是平行四边形,得BC1∥AD1,
由此可得∠D1AC(或补角)就是异面直线AC与BC1所成角.
∵△AD1C是等边三角形,
∴∠D1AC=60°,即异面直线AC与BC1所成角的大小为60°.


【解析】(1)利用线面平行的判定定理进行证明.(2)连结AD1、CD1 , 可证出四边形ABC1D1是平行四边形,得BC1∥AD1 , 得∠D1AC(或补角)就是异面直线AC与BC1所成角.等边△AD1C中求出∠D1AC=60°,即得异面直线AC与BC1所成角的大小.
【考点精析】利用异面直线及其所成的角和直线与平面平行的判定对题目进行判断即可得到答案,需要熟知异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
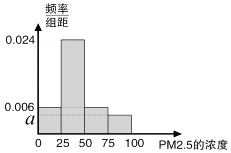
阳光课堂同步练习系列答案【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表
组别 | PM2.5浓度 | 频数(天) | 频率 |
第一组 | (0,25] | 3 | 0.15 |
第二组 | (25,50] | 12 | 0.6 |
第三组 | (50,75] | 3 | 0.15 |
第四组 | (75,100] | 2 | 0.1 |
(1)从样本中PM2.5的24小时平均浓度超过50微克/立方米的天数中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(2)将这20天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图. ①求图中a的值;
②求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.