题目内容
【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表
组别 | PM2.5浓度 | 频数(天) | 频率 |
第一组 | (0,25] | 3 | 0.15 |
第二组 | (25,50] | 12 | 0.6 |
第三组 | (50,75] | 3 | 0.15 |
第四组 | (75,100] | 2 | 0.1 |
(1)从样本中PM2.5的24小时平均浓度超过50微克/立方米的天数中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(2)将这20天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图. ①求图中a的值;
②求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.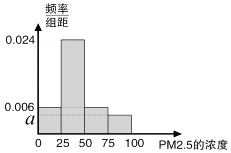
【答案】
(1)解:设PM2.5的24小时平均浓度在(50,75]内的三天记为A1,A2,A3,
PM2.5的24小时平均浓度在(75,100)内的两天记为B1,B2.
所以5天任取2天的情况有:
A1A2,A1A3,A1B1,A1B2,A2A3,A2B1,A2B2,A3B1,A3B2共10种.
其中符合条件的有:A1B1,A1B2,A2B1,A2B2,A3B1,A3B2共6种
所以所求的概率P= ![]() =
= ![]()
(2)解:①由第四组的频率为:0.1得:25a=0.1,
解得:a=0.004
②去年该居民区PM2.5年平均浓度为:12.5×0.15+37.5×0.6+62.5×0.15+87.5×0.1=42.5(微克/立方米).
因为42.5>35,
所以去年该居民区PM2.5年平均浓度不符合环境空气质量标准,故该居民区的环境需要改进
【解析】(1)设PM2.5的24小时平均浓度在(50,75]内的三天记为A1 , A2 , A3 , PM2.5的24小时平均浓度在(75,100)内的两天记为B1 , B2 , 求出基本事件总数,符合条件的基本事件总数,即可求得概率;(2)①由第四组的频率为:0.1得:25a=0.1,解得a值;②利用组中值×频数,可得去年该居民区PM2.5年平均浓度,进而可判断该居民区的环境是否需要改进.
【考点精析】利用频率分布直方图对题目进行判断即可得到答案,需要熟知频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.

【题目】《最强大脑》是大型科学竞技类真人秀节目,是专注传播脑科学知识和脑力竞技的节目.某机构为了了解大学生喜欢《最强大脑》是否与性别有关,对某校的100名大学生进行了问卷调查,得到如下列联表:
喜欢《最强大脑》 | 不喜欢《最强大脑》 | 合计 | |
男生 | 15 | ||
女生 | 15 | ||
合计 |
已知在这100人中随机抽取1人抽到不喜欢《最强大脑》的大学生的概率为0.4
( I)请将上述列联表补充完整;判断是否有99.9%的把握认为喜欢《最强大脑》与性别有关,并说明理由;
( II)已知在被调查的大学生中有5名是大一学生,其中3名喜欢《最强大脑》,现从这5名大一学生中随机抽取2人,抽到喜欢《最强大脑》的人数为X,求X的分布列及数学期望.
下面的临界值表仅参考:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2=![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)