题目内容
【题目】如图所示，△ACD是边长为1的等边三角形，△ABC是等腰直角三角形，∠ACB=90°，BD交AC于点E．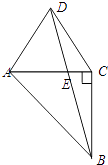 
（1）求BD2的值；
（2）求线段AE的长．
【答案】
（1）解：在△BCD中，CD=CB=1，∠DCB=150°，∠CDB=∠CBD=15°
由余弦定理可得：BD2=1+1﹣2×1×1×cos150°=2+ 
（2）解：在△ADE中，AD=1，∠DAE=60°，∠ADE=45°，则∠AED=75°
由正弦定理可得： 
∴AE= 
【解析】（1）在△BCD中，CD=CB=1，∠DCB=150°，∠CDB=∠CBD=15°，利用余弦定理可求BD2；（2）在△ADE中，AD=1，∠DAE=60°，∠ADE=45°，则∠AED=75°，由正弦定理可得AE的值．
练习册系列答案
精英口算卡系列答案
相关题目
【题目】4月23日是世界读书日，惠州市某中学在此期间开展了一系列的读书教育活动。为了解本校学生课外阅读情况，学校随机抽取了100名学生对其课外阅读时间进行调查。下面是根据调查结果绘制的学生日均课外阅读时间(单位：分钟)的频率分布直方图，且将日均课外阅读时间不低于60分钟的学生称为“读书迷”，低于60分钟的学生称为“非读书迷”．
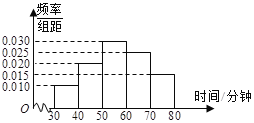
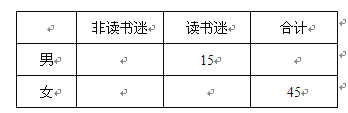
（Ⅰ）根据已知条件完成下面2×2列联表，并据此判断是否有99%的把握认为“读书迷”与性别有关？
（Ⅱ）将频率视为概率，现在从该校大量学生中用随机抽样的方法每次抽取1人，共抽取3次，记被抽取的3人中“读书迷”的人数为
，若每次抽取的结果是相互独立的，求
的分布列、数学期望
和方差
．
附：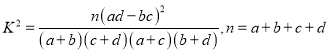 
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
