题目内容
【题目】已知圆![]() ,定点
,定点![]() 为圆上一动点,线段
为圆上一动点,线段![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() ;
;
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)若经过![]() 的直线
的直线![]() 交曲线于不同的两点
交曲线于不同的两点![]() ,(点
,(点![]() 在点
在点![]() ,
, ![]() 之间),且满足
之间),且满足![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(1) ![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线, ![]() ,
, ![]() 轨迹方程;(2)设直线
轨迹方程;(2)设直线![]() 的方程为:
的方程为: ![]() ,联立方程得:
,联立方程得: ![]() ,
, 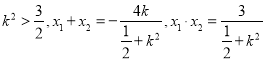 ,由
,由![]() ,得
,得![]() ,巧借韦达定理建立
,巧借韦达定理建立![]() 的方程,解之即可.
的方程,解之即可.
试题解析:
(Ⅰ)设点![]() 的坐标为
的坐标为![]() ,
,
![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线, ![]() ,
,
又点![]() 在
在![]() 上,圆
上,圆![]() ,半径是
,半径是![]()
![]()
![]() 点
点![]() 的轨迹是以
的轨迹是以![]() 为焦点的椭圆,
为焦点的椭圆,
设其方程为![]() ,则
,则
![]()
![]() 曲线
曲线![]() 方程:
方程: ![]()
(Ⅱ)设![]()
当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() 的斜率为
的斜率为![]()
则直线![]() 的方程为:
的方程为: ![]() ,
,
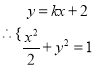 ,整理得:
,整理得: ![]() ,
,
由![]() ,解得:
,解得: 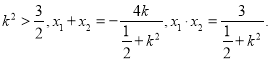 ------①
------①
又![]() ,
,
由![]() ,得
,得![]() ,结合①得
,结合①得
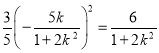 ,即
,即![]() ,
,
解得![]()
![]() 直线
直线![]() 的方程为:
的方程为: ![]() ,
,
当直线![]() 斜率不存在时,直线
斜率不存在时,直线![]() 的方程为
的方程为![]() 与
与![]() 矛盾.
矛盾.
![]() 直线
直线![]() 的方程为:
的方程为:

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
【题目】4月23日是世界读书日,惠州市某中学在此期间开展了一系列的读书教育活动。为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查。下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,且将日均课外阅读时间不低于60分钟的学生称为“读书迷”,低于60分钟的学生称为“非读书迷”.
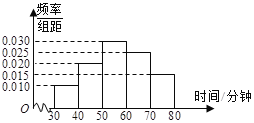
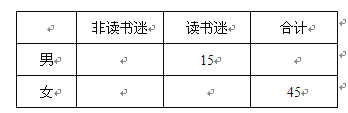
(Ⅰ)根据已知条件完成下面2×2列联表,并据此判断是否有99%的把握认为“读书迷”与性别有关?
(Ⅱ)将频率视为概率,现在从该校大量学生中用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中“读书迷”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列、数学期望
的分布列、数学期望![]() 和方差
和方差![]() .
.
附: 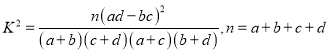
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |