题目内容
【题目】请从下面三个条件中任选一个,补充在下面的横线上,并作答.
①AB⊥BC,②FC与平面ABCD所成的角为![]() ,③∠ABC
,③∠ABC![]() .
.
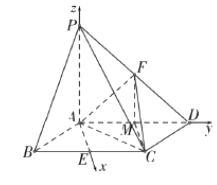
如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,PA⊥平面ABCD,且PA=AB=2,,PD的中点为F.
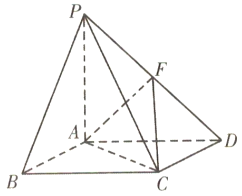
(1)在线段AB上是否存在一点G,使得AF![]() 平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
(2)若_______,求二面角F﹣AC﹣D的余弦值.
【答案】(1)存在,G是线段AB的中点,证明见解析;(2)详见解析
【解析】
(1)设PC的中点为H,连结FH,由题意得AGHF为平行四边形,则AF∥GH,由此能证明在线段AB上存在中点G,使得AF∥平面PCG.
(2)选择①AB⊥BC,推导出AB,AD,AP彼此两两垂直,以AB,AD,AP分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角F﹣AC﹣D的余弦值.选择②FC与平面ABCD所成的角为![]() ,取BC中点E,连结AE,取AD的中点M,连结FM,CM,则FM∥PA,且FM=1,FM⊥平面ABCD,FC与平面ABCD所成角为∠FCM,
,取BC中点E,连结AE,取AD的中点M,连结FM,CM,则FM∥PA,且FM=1,FM⊥平面ABCD,FC与平面ABCD所成角为∠FCM,![]() ,推导出AE,AD,AP彼此两两垂直,以AE、AD、AP分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角F﹣AC﹣D的余弦值.选择③∠ABC
,推导出AE,AD,AP彼此两两垂直,以AE、AD、AP分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角F﹣AC﹣D的余弦值.选择③∠ABC![]() ,推导出PA⊥BC,取BC中点E,连结AE,推导出 AE,AD,AP彼此两两垂直,以AE、AD、AP分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角F﹣AC﹣D的余弦值.
,推导出PA⊥BC,取BC中点E,连结AE,推导出 AE,AD,AP彼此两两垂直,以AE、AD、AP分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角F﹣AC﹣D的余弦值.
(1)在线段AB上存在中点G,使得AF∥平面PCG.
证明如下:如图所示:

设PC的中点为H,连结FH,
因为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]()
所以四边形AGHF为平行四边形,
则AF∥GH,
又GH平面PGC,AF平面PGC,
∴AF∥平面PGC.
(2)选择①AB⊥BC:
∵PA⊥平面ABCD,∴PA⊥BC,
由题意知AB,AD,AP彼此两两垂直,
以AB,AD,AP分别为x,y,z轴,建立空间直角坐标系,
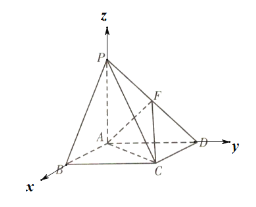
∵PA=AB=2,
则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),F(0,1,1),P(0,0,2),
∴![]() (0,1,1),
(0,1,1),![]() (﹣2,﹣1,1),
(﹣2,﹣1,1),
设平面FAC的一个法向量为![]() (x,y,z),
(x,y,z),
∴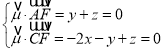 ,
,
取y=1,得![]() (﹣1,1,﹣1),
(﹣1,1,﹣1),
平面ACD的一个法向量为![]() (0,0,1),
(0,0,1),
设二面角F﹣AC﹣D的平面角为θ,
则cosθ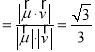 ,
,
∴二面角F﹣AC﹣D的余弦值为![]() .
.
选择②FC与平面ABCD所成的角为![]() :
:
∵PA⊥平面ABCD,取BC中点E,连结AE,取AD的中点M,连结FM,CM,
则FM∥PA,且FM=1,
∴FM⊥平面ABCD,
FC与平面ABCD所成角为∠FCM,∴![]() ,
,
在Rt△FCM中,CM![]() ,
,
又CM=AE,∴AE2+BE2=AB2,∴BC⊥AE,
∴AE,AD,AP彼此两两垂直,
以AE、AD、AP分别为x,y,z轴,建立空间直角坐标系,
∵PA=AB=2,
∴A( 0,0,0),B( ![]() ,﹣1,0),C(
,﹣1,0),C(![]() ,1,0),D(0,2,0),E(
,1,0),D(0,2,0),E(![]() ,0,0),F(0,1,1),P(0,0,2),
,0,0),F(0,1,1),P(0,0,2),
∴![]() (0,1,1),
(0,1,1),![]() (
(![]() ,0,1),
,0,1),
设平面EAC的一个法向量为![]() (x,y,z),
(x,y,z),
则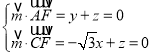 ,
,
取x![]() ,得
,得![]() (
(![]() ,﹣3,3),
,﹣3,3),
平面ACD的一个法向量为:![]() (0,0,1),
(0,0,1),
设二面角F﹣AC﹣D的平面角为θ,
则cosθ .
.
∴二面角F﹣AC﹣D的余弦值为![]() .
.
选择③∠ABC![]() :
:
∵PA⊥平面ABCD,
∴PA⊥BC,取BC中点E,连结AE,
∵底面ABCD是菱形,∠ABC=60°,∴△ABC是正三角形,
∵E是BC的中点,∴BC⊥AE,
∴AE,AD,AP彼此两两垂直,
以AE、AD、AP分别为x,y,z轴,建立空间直角坐标系,
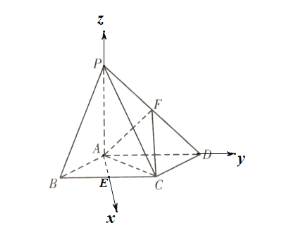
∵PA=AB=2,
∴A( 0,0,0),B( ![]() ,﹣1,0),C(
,﹣1,0),C(![]() ,1,0),D(0,2,0),E(
,1,0),D(0,2,0),E(![]() ,0,0),F(0,1,1),P(0,0,2),
,0,0),F(0,1,1),P(0,0,2),
∴![]() (0,1,1),
(0,1,1),![]() (
(![]() ,0,1),
,0,1),
设平面EAC的一个法向量为![]() (x,y,z),
(x,y,z),
则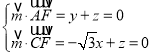 ,
,
取x![]() ,得
,得![]() (
(![]() ,﹣3,3),
,﹣3,3),
平面ACD的法向量![]() (0,0,1),
(0,0,1),
设二面角F﹣AC﹣D的平面角为θ,
θ则cosθ .
.
∴二面角F﹣AC﹣D的余弦值为![]() .
.